题目内容
4．正六边形的每个内角等于120°．分析 根据多边形内角和公式即可求出答案．
解答 解：六边形的内角和为：（6-2）×180°=720°，
∴正六边形的每个内角为：$\frac{720°}{6}$=120°，
故答案为：120°
点评 本题考查多边形的内角和，解题的关键是求出六边形的内角和，本题属于基础题型．
练习册系列答案
相关题目
15．
为了了解某校九年级学生的跳高水平，随机抽取该年级50名学生进行跳高测试，并把测试成绩绘制成如图所示的频数表和未完成的频数直方图（每组含前一个边界值，不含后一个边界值）．
某校九年级50名学生跳高测试成绩的频数表
（1）求a的值，并把频数直方图补充完整；
（2）该年级共有500名学生，估计该年级学生跳高成绩在1.29m（含1.29m）以上的人数．
为了了解某校九年级学生的跳高水平，随机抽取该年级50名学生进行跳高测试，并把测试成绩绘制成如图所示的频数表和未完成的频数直方图（每组含前一个边界值，不含后一个边界值）．某校九年级50名学生跳高测试成绩的频数表
| 组别（m） | 频数 |
| 1.09～1.19 | 8 |
| 1.19～1.29 | 12 |
| 1.29～1.39 | a |
| 1.39～1.49 | 10 |
（2）该年级共有500名学生，估计该年级学生跳高成绩在1.29m（含1.29m）以上的人数．
如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y轴分别相交于M（4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．
19．
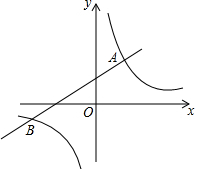如图，在平面直角坐标系xOy中，函数y=kx+b（k≠0）与y=$\frac{m}{x}$（m≠0）的图象相交于点A（2，3），B（-6，-1），则不等式kx+b＞$\frac{m}{x}$的解集为（ ）
如图，在平面直角坐标系xOy中，函数y=kx+b（k≠0）与y=$\frac{m}{x}$（m≠0）的图象相交于点A（2，3），B（-6，-1），则不等式kx+b＞$\frac{m}{x}$的解集为（ ）| A． | x＜-6 | B． | -6＜x＜0或x＞2 | C． | x＞2 | D． | x＜-6或0＜x＜2 |
如图是一个由4个相同的正方体组成的立体图形，它的主视图是（ ）
