题目内容
5.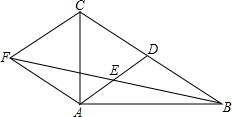 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.(1)求证:四边形ADCF是平行四边形;
(2)当AB=AC时,求证四边形ADCF是矩形;
(3)当△ABC满足什么条件时,四边形ADCF是菱形?并证明你的结论.
分析 (1)首先利用全等三角形的判定方法得出△AEF≌△DEB(AAS),进而得出AF=BD,再利用一组对边平行且相等的四边形是平行四边形进而得出答案;
(2)由AB=AC,根据三线合一的性质,可得AD⊥BC,继而可得四边形ADCF是矩形;
(3)根据∠BAC=90°,AD是BC边上的中线,从而得到AD=$\frac{1}{2}$BC=DC,然后利用邻边相等的平行四边形是菱形即可得到结论.
解答 证明:(1)∵AF∥BC,
∴∠AFE=∠EBD.
在△AEF和△DEB中
$\left\{\begin{array}{l}{∠AFE=∠DBE}\\{∠FEA=∠BED}\\{AE=DE}\end{array}\right.$,
∴△AEF≌△DEB(AAS).
∴AF=BD.
∴AF=DC.
又∵AF∥BC,
∴四边形ADCF为平行四边形;
(2)∵AB=AC,AD是中线,
∴AD⊥BC,
∵四边形ADCF是平行四边形,
∴四边形ADCF是矩形;
(3)当∠BAC=90°时,四边形ADCF是菱形.
证明:∵∠BAC=90°,AD是BC边上的中线,
∴AD=$\frac{1}{2}$BC=DC,
∵四边形ADCF是平行四边形,
∴平行四边形ADCF是菱形.
点评 本题考查了平行四边形的判定、菱形的判定及矩形的判定的知识,解题的关键是牢记几个判定定理,难度不大.

练习册系列答案
相关题目
13.据统计,2015年我国手机上网人数约为6.20亿,数据6.20亿用科学记数法表示为( )
| A. | 0.620×1011 | B. | 6.20×1010 | C. | 6.20×109 | D. | 6.20×108 |
14.圆心角为240°的扇形的半径为3cm,则这个扇形的面积是( )
| A. | πcm2 | B. | 3πcm2 | C. | 9πcm2 | D. | 6πcm2 |
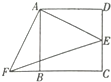 如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF.
如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF. 如图,点B、C在直线AD上,∠ABE=70°,BF平分∠DBE,CG∥BF,求∠DCG的度数.
如图,点B、C在直线AD上,∠ABE=70°,BF平分∠DBE,CG∥BF,求∠DCG的度数.
 如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.
如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.