题目内容
8.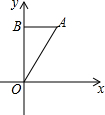 如图:在平面直角坐标系中,点A的坐标(2,4),点B的坐标(0,4),将△AOB绕点O旋转90°至△COD位置(其中点C与点A是对应点,点D与点B是对应点),OD落在x轴上,则点C的坐标是(4,-2),(-4,2).
如图:在平面直角坐标系中,点A的坐标(2,4),点B的坐标(0,4),将△AOB绕点O旋转90°至△COD位置(其中点C与点A是对应点,点D与点B是对应点),OD落在x轴上,则点C的坐标是(4,-2),(-4,2).
分析 根据旋转的性质得到对应边相等从而得到点到坐标轴的距离,即可得到结果.
解答 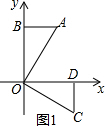 解:∵A的坐标(2,4),点B的坐标(0,4),
解:∵A的坐标(2,4),点B的坐标(0,4),
∴OB=4,AB=2,
①△AOB绕点O顺时针旋转90°至△COD位置,如图1,
根据旋转的性质得:OD=OB=4,CD=AB=2,
∴C(4,-2);
②△AOB绕点O逆时针旋转90°至△COD位置,如图2,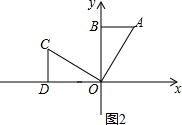
根据旋转的性质得:OD=OB=4,CD=AB=2,
∴C(-4,2);
综上所述:C(4,-2),(-4,2).
故答案为:(4,-2),(-4,2).
点评 本题考查了坐标与图形的变换-旋转的性质,熟练掌握旋转的性质是解题的关键.

练习册系列答案
相关题目
13.有四根细木棒,长度分别为3cm,5cm,7cm,9cm,则随机抽出三根木棒,能够组成三角形的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
20.如表是某校八年级(8)班共50位同学身高情况的频数分布表,则表中的组距是7,身高最大值与最小值的差至多是27cm.
| 组别(cm) | 145.5~152.5 | 152.5~159.5 | 159.5~166.5 | 166.5~173.5 |
| 频数(人) | 9 | 19 | 14 | 8 |
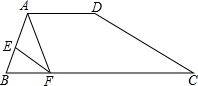 如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.
如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.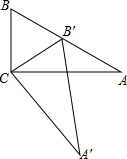 如图,在△ABC中,∠ACB=90°,∠B=60°,以C为旋转中心,旋转一定角度后成△A′B′C,此时B′落在斜边AB上,试确定∠ACA′,∠BB′C的度数.
如图,在△ABC中,∠ACB=90°,∠B=60°,以C为旋转中心,旋转一定角度后成△A′B′C,此时B′落在斜边AB上,试确定∠ACA′,∠BB′C的度数.