题目内容
17.如图1,在平面直角坐标系中,A(0,1),B(4,1),C为x轴上一点,且AC平分∠OAB.(1)求证:∠OAC=∠OCA;
(2)如图2,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于P点,及满足∠POC=$\frac{1}{3}$∠AOC,∠PCE=$\frac{1}{3}$∠ACE,求∠P的大小;
(3)如图3,在(2)中,若射线OP、CP满足∠POC=$\frac{1}{n}$∠AOC,∠PCE=$\frac{1}{n}$∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).

分析 (1)根据AB坐标可以求得∠OAB大小,根据角平分线性质可求得∠OAC大小,即可解题;
(2)根据题干中给出的∠POC=$\frac{1}{3}$∠AOC、∠PCE=$\frac{1}{3}$∠ACE可以求得∠PCE和∠POC的大小,再根据三角形外角等于不相邻两内角和即可解题;
(3)解法和(2)相同,根据题干中给出的∠POC=$\frac{1}{n}$∠AOC、∠PCE=$\frac{1}{n}$∠ACE可以求得∠PCE和∠POC的大小,再根据三角形外角等于不相邻两内角和即可解题.
解答 解:(1)∵A(0,1),B(4,1),
∴AB∥CO,
∴∠OAB=90°,
∵AC平分∠OAB.
∴∠OAC=45°,
∴∠OCA=90°-45°=45°,
∴∠OAC=∠OCA;
(2)∵∠POC=$\frac{1}{3}$∠AOC,∴∠POC=$\frac{1}{3}$×90°=30°,
∵∠PCE=$\frac{1}{3}$∠ACE,∴∠PCE=$\frac{1}{3}$(180°-45°)=45°,
∵∠P+∠POC=∠PCE,
∴∠P=∠PCE-∠POC=15°;
(3)∵∠POC=$\frac{1}{n}$∠AOC,∴∠POC=$\frac{1}{n}$×90°=$\frac{90}{n}$°,
∵∠PCE=$\frac{1}{n}$∠ACE,∴∠PCE=$\frac{1}{n}$(180°-45°)=$\frac{135}{n}$°,
∵∠P+∠POC=∠PCE,
∴∠P=∠PCE-∠POC=$\frac{45}{n}$°.
点评 本题考查了三角形内角和为180°的性质,考查了角平分线平分角的性质,考查了三角形外角等于不相邻两内角和的性质,本题中求∠PCE和∠POC的大小是解题的关键.

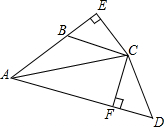 如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,E是AB延长线上一点,且CE⊥AE,CF⊥AD.
如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,E是AB延长线上一点,且CE⊥AE,CF⊥AD.