题目内容
12.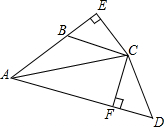 如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,E是AB延长线上一点,且CE⊥AE,CF⊥AD.
如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,E是AB延长线上一点,且CE⊥AE,CF⊥AD.(1)求证:BE=DF;
(2)试探究线段AB、AD、AF之间的数量关系,并说明理由.
分析 (1)根据角平分线的性质可得到CE=CF,根据余角的性质可得到∠EBC=∠D,已知CE⊥AB,CF⊥AD,从而利用AAS即可判定△CBE≌△CDF即可解决问题;
(2)已知EC=CF,AC=AC,则根据HL判定△ACE≌△ACF得AE=AF,最后证得AB+AD=2AF即可.
解答 (1)证明:∵AC平分∠BAD,CE⊥AB,CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°,∠ABC+∠EBC=180°
∴∠EBC=∠D
∵∠CEB=∠CFD=90°
∴△CBE≌△CDF,
∴BE=DF.
(2)解:结论:AB+AF=2AF,
理由:∵CE=CF,AC=AC
∴△ACE≌△ACF
∴AE=AF,∵BE=DF.
∴AB+AD=AE-BE+AF+DF=2AF.
点评 本题考查了全等三角形的判定和性质;证明线段相等往往通过三角形全等来证明,还要运用相等的线段进行转移,这是很重要的方法,注意掌握.

练习册系列答案
相关题目
9.下列图形中,△ABC与△DEF不一定相似的是( )
| A. |  | B. |  | C. |  | D. |  |
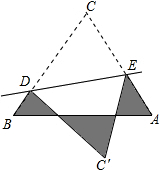 如图,在△ABC中,AC=BC=4cm,AB=6cm,D、E分别是BC、AC上的点,将△CDE沿直线DE折叠,点C落在点C′处,且C′在△ABC外部,则阴影部分图形的周长为14cm.
如图,在△ABC中,AC=BC=4cm,AB=6cm,D、E分别是BC、AC上的点,将△CDE沿直线DE折叠,点C落在点C′处,且C′在△ABC外部,则阴影部分图形的周长为14cm. (1)已知:如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点,求线段MN的长度.
(1)已知:如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点,求线段MN的长度. 如图,C是线段AB上一点,M是线段AC的中点,若AB=10cm,BC=3cm,求线段MB的长.
如图,C是线段AB上一点,M是线段AC的中点,若AB=10cm,BC=3cm,求线段MB的长.