题目内容
2.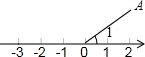 如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少?
如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少?
分析 分三种情况讨论:①当OP=OA时;②当OP=PA时;③当AP=A0时;然后根据等腰三角形的性质,求出P点的坐标即可.
解答  解:如图,①当OP=OA=2时,
解:如图,①当OP=OA=2时,
∴P点的坐标是P(2,0)或(-2,0).
②当OP=PA时,作PD⊥x轴于D,
∵∠1=30°,
∴OD=$\frac{\sqrt{3}}{2}$OA=$\sqrt{3}$,
∴OP=2$\sqrt{3}$,
∴P(2$\sqrt{3}$,0);
③当AP=A0时,则OP=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2}{3}$$\sqrt{3}$,
∴P($\frac{2}{3}$$\sqrt{3}$,0).
综上,P点的坐标是(2,0)、(-2,0)、(2$\sqrt{3}$,0)或($\frac{2}{3}$$\sqrt{3}$,0);将∠1=30°改为45°则P点的坐标为(2,0)、(-2,0)、(2$\sqrt{2}$,0)或($\sqrt{2}$,0);将∠1=30°改为60°则P点的坐标为(2,0)、(-2,0).
点评 本题考查了等腰三角形的判定和性质以及直角三角函数,分类讨论思想的运用是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列函数中,当x<0时,y随x的增大而减小的是( )
| A. | y=$\frac{3}{4}$x | B. | y=x-1 | C. | y=x2 | D. | y=-x2 |
10.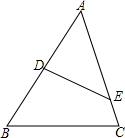 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )| A. | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C. | ∠AED=∠B | D. | ∠AED=∠C |
7.下列从左到右的变形,属于因式分解的是( )
| A. | a(a-b)=a2-ab | B. | (x+1)(x-1)=x2-1 | C. | x2-4y2=(x+4y)(x-4y) | D. | (x-1)(x-3)+1=(x-2)2 |
11.已知方程2x2-4x-3=0两根分别是x1和x2,则x1x2的值等于( )
| A. | -3 | B. | -$\frac{3}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
 如图,AB=AC,∠B=40°,点D在BC上,且∠DAC=50°.求证:BD=CD.
如图,AB=AC,∠B=40°,点D在BC上,且∠DAC=50°.求证:BD=CD. 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为6.
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为6. 如图,把两条钢条的中点连在一起,可以做成一个测量工件槽宽的工具(卡钳).那么要测量工件内槽宽A′B′,则只要测量AB即可.
如图,把两条钢条的中点连在一起,可以做成一个测量工件槽宽的工具(卡钳).那么要测量工件内槽宽A′B′,则只要测量AB即可.