题目内容
10.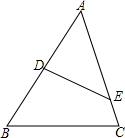 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )| A. | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C. | ∠AED=∠B | D. | ∠AED=∠C |
分析 根据已知及相似三角形的判定方法进行分析,从而得到答案.
解答 解:A、虽然$\frac{AD}{AC}=\frac{DE}{BC}$,但∠A不为夹角,
不符合三角形相似的判定方法;
B、∵$\frac{AD}{AC}=\frac{AE}{AB}$,∠A=∠A,
∴△AED∽△ABC;
C、∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC;
D、∵∠ADE=∠C,∠A=∠A,
∴△AED∽△ABC;
故选:A.
点评 本题考查了相似三角形的判定方法;三角形相似有多种判断方法,要灵活运用,且一定注意各元素的位置关系.

练习册系列答案
相关题目
20.由下列条件不能判定△ABC为直角三角形的是( )
| A. | ∠A+∠C=∠B | B. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | C. | (b+a)(b-a)=c2 | D. | ∠A:∠B:∠C=5:3:2 |
18.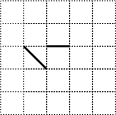 在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )
在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )
 在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )
在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
5.方程x=-x(x+1)的解是( )
| A. | x=-2 | B. | x=0 | C. | x1=-1,x2=0 | D. | x1=-2,x2=0 |
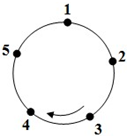 如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.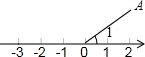 如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少?
如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少? 如图所示,在方格纸上建立的平面直角坐标系中:
如图所示,在方格纸上建立的平面直角坐标系中: