题目内容
 如图:在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线Ln,它们的顶点Cn(Xn,Yn)在直线AB上,并且经过点(Xn+1,0),当n=1,2,3,4,5…时,Xn=2,3,5,8,13…,根据上述规律,写出抛物线L1的表达式为
如图:在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线Ln,它们的顶点Cn(Xn,Yn)在直线AB上,并且经过点(Xn+1,0),当n=1,2,3,4,5…时,Xn=2,3,5,8,13…,根据上述规律,写出抛物线L1的表达式为考点:二次函数图象与几何变换
专题:规律型
分析:根据A(-2,0),B(0,1)的坐标求直线AB的解析式为y=
x+1,因为顶点C1的在直线AB上,C1坐标可求;根据横坐标的变化规律可知,C6的横坐标为21,代入直线AB的解析式y=
x+1中,可求纵坐标.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设直线AB的解析式为y=kx+b(k≠0).
则
,
解得
,
∴直线AB的解析式为y=
x+1
∵抛物线L1的顶点C1的横坐标为2,且顶点在直线AB上,
∴y1=
×2+1=2.
则C1(2,2).
故设抛物线L1的表达式为y=a(x-2)2+2(a≠0).
又∵该抛物线经过点(3,0),
∴0=a(3-2)2+2,
解得 a=-2.
故抛物线L1的表达式为y=-2(x-2)2+2或y=-2x2+8x-6.
∵对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…
∴每个数都是前两个数的和
∴抛物线L6的顶点C6的横坐标为21,
则y6=
×21+1=
.
∴抛物线L6的顶点坐标为:(21,
).
同理,由抛物线L6经过点(22,0),求得该抛物线的解析式为:y=-
(x-2)2+
或y=-
x2+46x-
.
故答案是:y=-2(x-2)2+2或y=-2x2+8x-6;(21,
);y=-
(x-2)2+
或y=-
x2+46x-
.
则
|
解得
|
∴直线AB的解析式为y=
| 1 |
| 2 |
∵抛物线L1的顶点C1的横坐标为2,且顶点在直线AB上,
∴y1=
| 1 |
| 2 |
则C1(2,2).
故设抛物线L1的表达式为y=a(x-2)2+2(a≠0).
又∵该抛物线经过点(3,0),
∴0=a(3-2)2+2,
解得 a=-2.
故抛物线L1的表达式为y=-2(x-2)2+2或y=-2x2+8x-6.
∵对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…
∴每个数都是前两个数的和
∴抛物线L6的顶点C6的横坐标为21,
则y6=
| 1 |
| 2 |
| 23 |
| 2 |
∴抛物线L6的顶点坐标为:(21,
| 23 |
| 2 |
同理,由抛物线L6经过点(22,0),求得该抛物线的解析式为:y=-
| 23 |
| 2 |
| 23 |
| 2 |
| 23 |
| 2 |
| 69 |
| 2 |
故答案是:y=-2(x-2)2+2或y=-2x2+8x-6;(21,
| 23 |
| 2 |
| 23 |
| 2 |
| 23 |
| 2 |
| 23 |
| 2 |
| 69 |
| 2 |
点评:此题考查了待定系数法求一次函数的解析式,还考查了点与函数关系式的关系,考查了学生的分析归纳能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知(a-1)2+
=0,则
+
+
+…+
值是( )
| b-2 |
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2015)(b+2015) |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
点A关于x轴对称的点的坐标为(m,-3),关于y轴对称的点的坐标(2,n),那么点A的坐标是( )
| A、(m,-n) |
| B、(-m,n) |
| C、(-3,2) |
| D、(-2,3) |
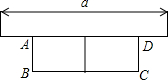 如图,有长为24米的篱笆,一边利用墙(墙的最大可用长度为3米),当花圃的宽AB为
如图,有长为24米的篱笆,一边利用墙(墙的最大可用长度为3米),当花圃的宽AB为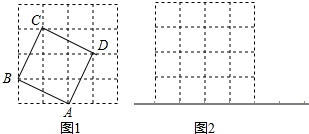 如图,4×4方格中每个小正方形的边长都为1.
如图,4×4方格中每个小正方形的边长都为1.