题目内容
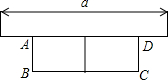如图，有长为24米的篱笆，一边利用墙（墙的最大可用长度为3米），当花圃的宽AB为考点：二次函数的最值
专题：
分析：设AB的长度为x米，则矩形ABCD的长BC=24-3x．利用矩形的面积公式列出函数关系式，利用二次函数的性质来求最值．
解答：解：设AB的长度为x米，面积为S米2，则
∵墙的最大可用长度为3米，
∴24-3x≤3，
解得 x≥7．
S=（24-3x）x=-3（x-4）2+48．
∵-3＜0，
∴函数S=-3（x-4）2+48的开口方向向下，
∴当x=7时，S最大=21．
故答案是：7；21．
∵墙的最大可用长度为3米，
∴24-3x≤3，
解得 x≥7．
S=（24-3x）x=-3（x-4）2+48．
∵-3＜0，
∴函数S=-3（x-4）2+48的开口方向向下，
∴当x=7时，S最大=21．
故答案是：7；21．
点评：本题考查了二次函数的最值．确定一个二次函数的最值，首先看自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值．
练习册系列答案
相关题目
如图，PA、PB分别切⊙O于A、B两点，射线PD与⊙O相交于C，D两点，点E是CD中点，若∠APB=40°，则∠AEP的度数是（ ）| A、40° | B、50° |
| C、60° | D、70° |
如图：在平面直角坐标系中，A（-2，0），B（0，1），有一组抛物线Ln，它们的顶点Cn（Xn，Yn）在直线AB上，并且经过点（Xn+1，0），当n=1，2，3，4，5…时，Xn=2，3，5，8，13…，根据上述规律，写出抛物线L1的表达式为
如图，等边△ABC的边长为8，点O为边AC的四等分点（AO＜CO），点P为边AB上一动点，连接OP．将△AOP绕点O逆时针旋转，得到△A′OP′，且使得点A′落在边AB上，当点P′落在边BC上时，则AP的长为
如图，在△ABC中，AB=5cm，BC=7cm，AC=8cm，⊙O和BC，AC，AB分别相切于D，E，F，求AF，BD和CE的长．