题目内容
9.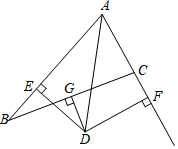 如图,在△ABC中,AB=7,AC=3,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F,下列说法正确的是( )
如图,在△ABC中,AB=7,AC=3,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F,下列说法正确的是( )①△ADE≌△ADF;②BE=CF;③AE=5.
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 根据角平分线的性质得DE=DF,则根据“HL”可证明Rt△ADE≌Rt△ADF;连接DB、DC,可判定DG垂直平分BC,则DB=DC,于是根据“HL”判断Rt△DBE≌Rt△DCF,所以BE=CF;利用Rt△ADE≌Rt△ADF得到AE=AF,则AB-BE=AC+CF,则计算出BE=CF=2,于是得到AE=5.
解答 解:∵AD平分∠BAC,DE⊥AB于E,DF⊥AC,
∴DE=DF,
在Rt△ADE和Rt△ADF中
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,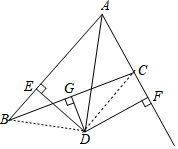
∴Rt△ADE≌Rt△ADF(HL),所以①正确;
连接DB、DC,
∵G为BC的中点,DG⊥BC
∴DG垂直平分BC,
∴DB=DC,
在Rt△DBE和Rt△DCF中
$\left\{\begin{array}{l}{DB=DC}\\{DE=DF}\end{array}\right.$,
∴Rt△DBE≌Rt△DCF(HL),
∴BE=CF,所以②正确;
∵Rt△ADE≌Rt△ADF,
∴AE=AF,
∴AB-BE=AC+CF,
即7-BE=3+BE,解得BE=2,
∴AE=AB-BE=7-2=5,所以③正确.
故选D.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了角平分线的性质和线段垂直平分线的性质.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1.下列说法错误的是( )
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{2}$是2的算术平方根 | D. | $\sqrt{(-3)^{2}}$的平方根是-3 |
18. 如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )
如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )
 如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )
如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,不能推出四边形ABCD是矩形的是( )| A. | BC=$\sqrt{3}$CD | B. | ∠A=90° | C. | AD=BC | D. | AB∥CD |
19.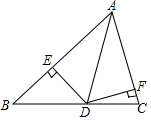 如图,AD是△ABC角平分线,DE⊥AB,DF⊥AC,垂足分别为点E和点F,则下列结论正确的是( )
如图,AD是△ABC角平分线,DE⊥AB,DF⊥AC,垂足分别为点E和点F,则下列结论正确的是( )
 如图,AD是△ABC角平分线,DE⊥AB,DF⊥AC,垂足分别为点E和点F,则下列结论正确的是( )
如图,AD是△ABC角平分线,DE⊥AB,DF⊥AC,垂足分别为点E和点F,则下列结论正确的是( )| A. | BD=CD | B. | AD=BD | C. | AD=CD | D. | DE=DF |
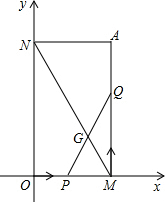 如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.
如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.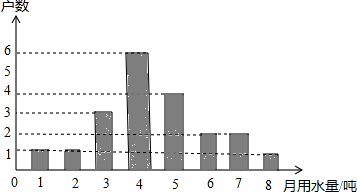 张小花是社区宣传干部,为宣传节约用水,他随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图的统计图.
张小花是社区宣传干部,为宣传节约用水,他随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图的统计图.