题目内容
8.学生队伍以每小时5千米的速度外出旅游,他们从学校出发走了4$\frac{1}{5}$小时后,学校就通讯员同学托车追赶学生队伍,传达紧急通知,通讯员用36分追赶上学生队伍,求摩托车的速度,设摩托车的速度为x千米/小时,那么方程是( )| A. | 36x=5(4$\frac{1}{5}$+36) | B. | $\frac{36}{60}$x=5×4$\frac{1}{5}$+$\frac{36}{60}$ | ||
| C. | $\frac{36}{60}$x=5(4$\frac{1}{5}$+$\frac{36}{60}$) | D. | $\frac{36}{60}$x=4$\frac{1}{5}$+5×$\frac{36}{60}$ |
分析 根据“摩托车行驶的路程=学生步行(4$\frac{1}{5}$+$\frac{36}{60}$)小时的路程”可列方程.
解答 解:设摩托车的速度为x千米/小时,则摩托车行驶的路程为$\frac{36}{60}$x千米,
根据题意,得:$\frac{36}{60}$x=5(4$\frac{1}{5}$+$\frac{36}{60}$),
故选:C.
点评 本题主要考查根据实际问题列一元一次方程的能力,解题的关键是理解题意得出两者在路程上的相等关系.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
19. 如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )
如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )
 如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )
如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )| A. | 24 | B. | 28 | C. | 32 | D. | 36 |
16. 在如图的正方形网格中,sin∠AOB的值为( )
在如图的正方形网格中,sin∠AOB的值为( )
 在如图的正方形网格中,sin∠AOB的值为( )
在如图的正方形网格中,sin∠AOB的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
3.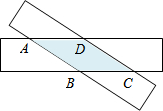 如图,把两条足够长的等宽的纸带交叉放置(不重合),重叠部分形成四边形ABCD,则四边形ABCD是( )
如图,把两条足够长的等宽的纸带交叉放置(不重合),重叠部分形成四边形ABCD,则四边形ABCD是( )
 如图,把两条足够长的等宽的纸带交叉放置(不重合),重叠部分形成四边形ABCD,则四边形ABCD是( )
如图,把两条足够长的等宽的纸带交叉放置(不重合),重叠部分形成四边形ABCD,则四边形ABCD是( )| A. | 平行四边形或矩形 | B. | 菱形或正方形 | ||
| C. | 平行四边形或正方形 | D. | 矩形或菱形 |
13. 如图,OB、OC是∠ABC、∠ACB的角平分线,∠BOC=120°,则∠A=( )
如图,OB、OC是∠ABC、∠ACB的角平分线,∠BOC=120°,则∠A=( )
 如图,OB、OC是∠ABC、∠ACB的角平分线,∠BOC=120°,则∠A=( )
如图,OB、OC是∠ABC、∠ACB的角平分线,∠BOC=120°,则∠A=( )| A. | 60° | B. | 120° | C. | 110° | D. | 40° |
20.三角形的三边长分别为a,b,c,且(a-b)2+(a2+b2-c2)2=0,则此三角形的形状为( )
| A. | 任意等腰三角形 | B. | 任意直角三角形 | C. | 任意三角形 | D. | 等腰直角三角形 |
17.数217×513的整数位数是( )
| A. | 17 | B. | 16 | C. | 15 | D. | 14 |
18. 如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
 如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )| A. | 16 | B. | 18 | C. | 19 | D. | 21 |