题目内容
3．
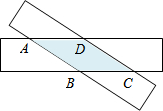如图，把两条足够长的等宽的纸带交叉放置（不重合），重叠部分形成四边形ABCD，则四边形ABCD是（ ）| A． | 平行四边形或矩形 | B． | 菱形或正方形 | ||
| C． | 平行四边形或正方形 | D． | 矩形或菱形 |
分析 四条边相等的四边形即为菱形，邻边相互垂直的菱形为正方形．
解答 
解：①当AB与BC不垂直时，如图所示：∵依题意可知AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，
分别作CD，BC边上的高为AE，AF，
∵两纸条相同，
∴纸条宽度AE=AF，
∵平行四边形的面积为AE×CD=BC×AF，
∴CD=BC，
∴平行四边形ABCD为菱形．
②同理，当AB⊥BC时，菱形ABCD为正方形．
综上所述，四边形ABCD是菱形或正方形．
故选：B．
点评 本题考查了正方形（菱形）的性质和判定，面积公式的综合运用，能正确作出辅助线是解此题的关键．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
14．
如图，两个天平都平衡，则与2个球体相等质量的正方体的个数为（ ）
如图，两个天平都平衡，则与2个球体相等质量的正方体的个数为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
11．下列从左边到右边的变形，因式分解正确的是（ ）
| A． | 2a2-2=2（a+1）（a-1） | B． | （a+3）（a-3）=a2-9 | ||
| C． | -ab2+2ab-3b=-b（ab-2a-3） | D． | x2-2x-3=x（x-2）-3 |
18．$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为（ ）
| A． | 1 | B． | $\frac{{2}^{n-2}}{{2}^{n}}$ | C． | 1-$\frac{1}{{2}^{n}}$ | D． | $\frac{{2}^{n}-1}{2n}$ |
8．学生队伍以每小时5千米的速度外出旅游，他们从学校出发走了4$\frac{1}{5}$小时后，学校就通讯员同学托车追赶学生队伍，传达紧急通知，通讯员用36分追赶上学生队伍，求摩托车的速度，设摩托车的速度为x千米/小时，那么方程是（ ）
| A． | 36x=5（4$\frac{1}{5}$+36） | B． | $\frac{36}{60}$x=5×4$\frac{1}{5}$+$\frac{36}{60}$ | ||
| C． | $\frac{36}{60}$x=5（4$\frac{1}{5}$+$\frac{36}{60}$） | D． | $\frac{36}{60}$x=4$\frac{1}{5}$+5×$\frac{36}{60}$ |
15．一个商人将99颗弹子放进两个盒子，每个大盒子装12个，每个小盒子装5个，恰好装完．盒子总个数大于9，问大小盒子各几个？（ ）
| A． | 大的2个，小的15个 | |
| B． | 大的7个，小的3个 | |
| C． | 大的2个，小的15个或 大的7个，小的3个 | |
| D． | 无数种 |
