题目内容
16. 在如图的正方形网格中,sin∠AOB的值为( )
在如图的正方形网格中,sin∠AOB的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
分析 先在∠AOB的两边上找出两点C、D,使△DOC构成直角三角形,再根据正方形网格的特点及勾股定理求出OC的长,由锐角三角函数的定义即可求出sin∠AOB的值.
解答 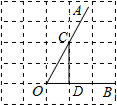 解:由图可知连接C、D两点,此时△DOC恰好构成直角三角形,
解:由图可知连接C、D两点,此时△DOC恰好构成直角三角形,
设正方形网格的边长为1,则CD=2,OD=1,OC=$\sqrt{C{D}^{2}+O{D}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
由锐角三角函数的定义可知:sin∠AOB=$\frac{CD}{OC}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
故选D.
点评 本题考查的是锐角三角函数的定义及勾股定理,熟知正方形网格的特点,能在∠AOB的边上找出两点使△DOC恰好构成直角三角形是解答此题的关键.

练习册系列答案
相关题目
6. 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE.
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE.
其中正确的结论是( )
 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE.
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE.其中正确的结论是( )
| A. | ①③ | B. | ②④ | C. | ①③④ | D. | ①②③④ |
11.下列从左边到右边的变形,因式分解正确的是( )
| A. | 2a2-2=2(a+1)(a-1) | B. | (a+3)(a-3)=a2-9 | ||
| C. | -ab2+2ab-3b=-b(ab-2a-3) | D. | x2-2x-3=x(x-2)-3 |
1.若式子3x+4的值不大于0,则x的取值范围是( )
| A. | x<-$\frac{4}{3}$ | B. | x≥$\frac{4}{3}$ | C. | x<$\frac{4}{3}$ | D. | x≤-$\frac{4}{3}$ |
8.学生队伍以每小时5千米的速度外出旅游,他们从学校出发走了4$\frac{1}{5}$小时后,学校就通讯员同学托车追赶学生队伍,传达紧急通知,通讯员用36分追赶上学生队伍,求摩托车的速度,设摩托车的速度为x千米/小时,那么方程是( )
| A. | 36x=5(4$\frac{1}{5}$+36) | B. | $\frac{36}{60}$x=5×4$\frac{1}{5}$+$\frac{36}{60}$ | ||
| C. | $\frac{36}{60}$x=5(4$\frac{1}{5}$+$\frac{36}{60}$) | D. | $\frac{36}{60}$x=4$\frac{1}{5}$+5×$\frac{36}{60}$ |
5.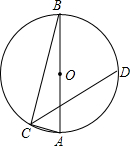 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=6,∠CBA=15°,则CD的长是( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=6,∠CBA=15°,则CD的长是( )
 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=6,∠CBA=15°,则CD的长是( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=6,∠CBA=15°,则CD的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 如图,在边长为3的正方形内有区域A(阴影部分所示),小明同学用随机模拟的方法求区域A的面积.若每次在正方形内随机产生10000个点,并记录落在区域A内的点的个数.经过多次试验,计算出落在区域A内点的个数平均值为6600个,则区域A的面积约为( )
如图,在边长为3的正方形内有区域A(阴影部分所示),小明同学用随机模拟的方法求区域A的面积.若每次在正方形内随机产生10000个点,并记录落在区域A内的点的个数.经过多次试验,计算出落在区域A内点的个数平均值为6600个,则区域A的面积约为( )