题目内容
19.已知关于x,y的方程组$\left\{\begin{array}{l}{x+y=3m+9}\\{x-y=5m+1}\end{array}\right.$的解为非负数,求m的取值范围.分析 先求出方程组的解,得出关于m的不等式组,求出不等式组的解集即可.
解答 解:解方程组$\left\{\begin{array}{l}{x+y=3m+9}\\{x-y=5m+1}\end{array}\right.$得:$\left\{\begin{array}{l}{x=4m+5}\\{y=-m+4}\end{array}\right.$,
∵关于x,y的方程组$\left\{\begin{array}{l}{x+y=3m+9}\\{x-y=5m+1}\end{array}\right.$的解为非负数,
∴$\left\{\begin{array}{l}{4m+5≥0}\\{-m+4≥0}\end{array}\right.$,
解得:-$\frac{5}{4}$≤m≤4,
即m的取值范围是-$\frac{5}{4}$≤m≤4.
点评 本题考查了解二元一次方程组,二元一次方程组的解,解一元一次不等式组等知识点,能得出关于m的不等式组是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.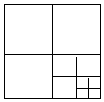 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2017}$ | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{1}{4}$)2017 | D. | 1-($\frac{1}{4}$)2017 |
10.已知|x|<a,x是整数,若满足条件的值有7个,则a的取值可能是( )
| A. | $\sqrt{8}$ | B. | π | C. | $\sqrt{17}$ | D. | 7 |
14.一次函数y=kx+3的图象与坐标轴围成的直角三角形的斜边长是5,且y的值随x值的增大而减小,则k的值为( )
| A. | 4 | B. | -4 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
11. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )
 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
 若关于x的不等式2x-m≥1的解集如图所示,则m=3.
若关于x的不等式2x-m≥1的解集如图所示,则m=3.