题目内容
16.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P,Q是边AC,BC上的两个动点,PD⊥AB于点D,QE⊥AB于点E,设点P,Q运动的时间是t秒(t>0).(1)若点P,Q分别从A,B两点同时出发,沿AC,BC向点C匀速运动,运动速度都为每秒1个单位,其中一点到达终点C后,另一点也随之停止运动,在运动过程中△APD和△QBE是否保持全等?判断并说明理由;
(2)若点P从点C出发沿CA以每秒3个单位的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q仍从点B出发沿BC以每秒1个单位的速度向点C匀速运动,到达点C后停止运动,当t为何值时,△APD和△QBE全等?
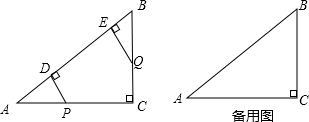
分析 (1)根据∠C=90°,PD⊥AB,QE⊥AB,于是得到∠A+∠APD=∠A+∠B=90°,证得∠APD=∠B,∠ADP=∠QEB=90°,即可得到结论;
(2)分两种情况:①0≤t$<\frac{8}{3}$时,点P从C到A运动,则AP=AC=CP=8-3t,BQ=t,求得t=2,②t$≥\frac{8}{3}$时,点P从A到C运动,则AP=3t-8,BQ=t,求得t=4.
解答 解:(1)△ADP≌△QBE,
理由:∵∠C=90°,PD⊥AB,QE⊥AB,
∴∠A+∠APD=∠A+∠B=90°,
∴∠APD=∠B,∠ADP=∠QEB=90°,
∵AP=BQ=t
,在△ADP与△QBE中,$\left\{\begin{array}{l}{∠APD=∠B}\\{∠ADP=∠QEB}\\{AP=BQ}\end{array}\right.$,
∴△ADP≌△QBE;
(2)①0≤t$<\frac{8}{3}$时,点P从C到A运动,则AP=AC=CP=8-3t,BQ=t,
当△ADP≌△QBE时,
则AP=BQ,
即8-3t=t,解得:t=2,
②t$≥\frac{8}{3}$时,点P从A到C运动,则AP=3t-8,BQ=t,
当△ADP≌△QBE时,
则AP=BQ,
即3t-8=t,
解得:t=4,
综上所述:当t=2s或4s时,△ADP≌△QBE.
点评 本题考查了全等三角形的判定,解方程,垂直的定义,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
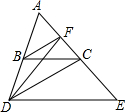 如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列判断:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD中,正确的有( )
如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列判断:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD中,正确的有( )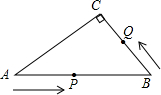 如图,在△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.设点P的运动时间为x(秒).
如图,在△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.设点P的运动时间为x(秒).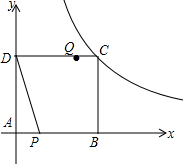 已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t. 如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).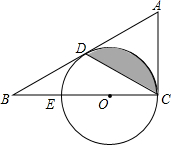 如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.
如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.