题目内容
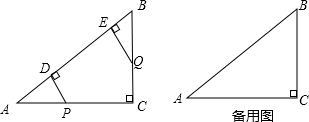
17. 如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列判断:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD中,正确的有( )
如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列判断:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD中,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平行线的性质求出∠ACB=∠E,根据角平分线定义和平行线的性质求出∠ABF=∠CBF=∠ADC=∠EDC,推出BF∥DC,再根据平行线的性质判断即可.
解答 解:∵BC∥DE,
∴∠ACB=∠E,∴①正确;
∵BC∥DE,
∴∠ABC=∠ADE,
∵BF平分∠ABC,DC平分∠ADE,
∴∠ABF=∠CBF=$\frac{1}{2}$∠ABC,∠ADC=∠EDC=$\frac{1}{2}$∠ADE,
∴∠ABF=∠CBF=∠ADC=∠EDC,
∴BF∥DC,
∴∠BFD=∠FDC,
当根据已知不能推出∠ADF=∠CDF,∴②错误;③错误;
∵∠ABF=∠ADC,∠ADC=∠EDC,
∴∠ABF=∠EDC,
∵DE∥BC,
∴∠BCD=∠EDC,
∴∠ABF=∠BCD,∴④正确;
即正确的有2个,
故选B.
点评 本题考查了平行线的性质和判定,角平分线定义的应用,能灵活运用平行线的性质和判定进行推理是解此题的关键.

练习册系列答案
相关题目
8.下列各题中,计算结果正确的是( )
| A. | 19a2b-9ab2=10ab | B. | 3x+3y=6xy | C. | 16y2-9y2=7 | D. | 3x-4x+5x=4x |
12.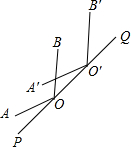 如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )
如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )
 如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )
如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |
 如图,点A是半圆上的三等分点,B是弧AN的中点,P是直径MN上一动点,⊙O的半径是1,问点P在直线MN上什么位置是(在图中标注),AP+BP的值最小?并求出最小值.
如图,点A是半圆上的三等分点,B是弧AN的中点,P是直径MN上一动点,⊙O的半径是1,问点P在直线MN上什么位置是(在图中标注),AP+BP的值最小?并求出最小值.
 如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1),
如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(-1,3),点C的坐标为(1,-1),