Question

17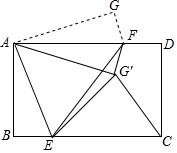．如图所示，矩形纸片ABCD中，AB=6，CB=8，现将纸片折叠压平，使A，C两点重合，折痕为EF，点D的对应点为G，再将△AGF沿着AF翻折，得△AG′F，连接EG′和CG′，则△EG′C的面积是$\frac{43}{4}$．

Answer 1

分析 先连接GG'并延长，交BC于Q，则GG'⊥AD，GQ⊥BC，GH=G'H，由折叠可得，DF=GF，AG=CD=6，∠CEF=∠AEF，由AD∥BC可得，∠CEF=∠AFE，进而得出AE=CE=AF，再根据勾股定理求得AF=CE=$\frac{25}{4}$，DF=GF=$\frac{7}{4}$，在Rt△AGF中，$\frac{1}{2}$×AG×GF=$\frac{1}{2}$×AF×GH，求得GH=$\frac{64}{25}$=G'H，进而得出G'Q=6-$\frac{64}{25}$=$\frac{86}{25}$，最后计算△EG′C的面积．

解答 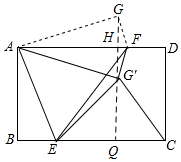解：连接GG'并延长，交BC于Q，则GG'⊥AD，GQ⊥BC，GH=G'H，
由折叠可得，DF=GF，AG=CD=6，∠CEF=∠AEF，
由AD∥BC可得，∠CEF=∠AFE，
∴∠AEF=∠AFE，
∴AE=CE=AF，
设AE=CE=AF=x，则DF=GF=8-x，
在Rt△AFG中，6²+（8-x）²=x²，
解得x=$\frac{25}{4}$，
∴AF=CE=$\frac{25}{4}$，DF=GF=$\frac{7}{4}$，
在Rt△AGF中，$\frac{1}{2}$×AG×GF=$\frac{1}{2}$×AF×GH，
∴$\frac{1}{2}$×6×$\frac{7}{4}$=$\frac{1}{2}$×$\frac{25}{4}$×GH，
∴GH=$\frac{42}{25}$=G'H，
∴G'Q=6-$\frac{42}{25}$=$\frac{108}{25}$，
∴△EG′C的面积=$\frac{1}{2}$×G'Q×CE=$\frac{1}{2}$×$\frac{108}{25}$×$\frac{25}{4}$=$\frac{27}{2}$．
故答案为：$\frac{27}{2}$．

点评 本题属于折叠问题，主要考查了轴对称的性质以及矩形的性质，勾股定理的综合应用，解决问题的关键是掌握：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．解题时注意方程思想和面积法的运用．