题目内容

12．如图是一次函数y=kx+b的图象，当y＜2时，x的取值范围是（　　）
A．x＜1B．x＞1C．x＜3D．x＞3

分析 根据一次函数图象与两坐标轴的交点坐标，利用待定系数法可求出一次函数解析式，再利用一次函数图象上点的坐标特征求出当y=2时的x值，观察函数图象即可得出结论．

解答 解：将（2，0）、（0，-4）代入y=kx+b，
$\left\{\begin{array}{l}{2k+b=0}\\{b=-4}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=2}\\{b=-4}\end{array}\right.$，
∴一次函数解析式为y=2x-4．
当y=2x-4=2时，x=3，
∴当x＜3时，y＜2．
故选C．

点评 本题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征，根据一次函数图象与两坐标轴的交点坐标，利用待定系数法求出一次函数解析式是解题的关键．

练习册系列答案
相关题目
2．从半径为10厘米的圆周上截下长为14.13厘米的弧，则此弧所对的圆心角是81 度．
3．比较大小：$\frac{5}{6}$＜$\frac{6}{7}$（填“＞”、“=”或“＜”=）．
20．[发现]如图∠ACB=∠ADB=90°，那么点D在经过A，B，C三点的圆上（如图①）

[思考]如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上吗？我们知道，如果点D不在经过A，B，C三点的圆上，那么点D要么在圆O外，要么在圆O内，以下该同学的想法说明了点D不在圆O外．（如图③，过A，B，C三点作圆，圆心为O，假设点D在圆O外，设AD交圆O于点E，连接BE，则∠AEB=∠ACB，又由∠AEB是△BDE的一个外角，得∠AEB＞∠ADB，因此∠ACB＞∠ADB，就与条件∠ACB=∠ADB矛盾，所以点D不在圆O外）
请结合图④证明点D也不在⊙O内．
[结论]综上可得结论：如图②，如果∠ACB=∠ADB=a（点C，D在AB的同侧），那么点D在经过A，B，C三点的圆上，即：点A、B、C、D四点共圆．
[应用]利用上述结论解决问题：
如图⑤，已知△ABC中，∠C=90°，将△ACB绕点A顺时针旋转一个角度得△ADE，连接BE、CD，延长CD交BE于点F，
（1）求证：点B、C、A、F四点共圆；
（2）求证：BF=EF．
7．已知等腰三角形的两角之差为30°，求该三角形各内角的度数．
17．如图，在?ABCD中，E为CD上一点，且DE：AB=2：5，联结AE、BD交于点F，若S△DEF=4，则S△ABF=25．
4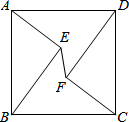．如图，在正方形ABCD中，AD=10，点E、F是正方形ABCD内的两点，且AE=FC=6，BE=DF=8，则EF的长为（　　）
A．2B．4C．$\frac{4}{3}$$\sqrt{2}$D．2$\sqrt{2}$
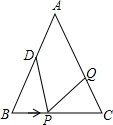1．如图，已知△ABC中，AB=AC=12厘米，BC=9厘米，点D为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B向C点运动，同时点Q在线段CA上由C点向A点运动．
（1）若点Q的运动速度与点P的运动速度相等，1秒钟时，△BPD与△CQP是否全等，请说明；
（2）点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD≌△CPQ？
2．二元一次方程2x+3y=18的正整数解共有多少组（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网