题目内容
7．已知等腰三角形的两角之差为30°，求该三角形各内角的度数．分析 设较小的内角是x，则较大的内角为x+30°，再分x是等腰三角形的底角或顶角两种情况求解即可．
解答 解：∵等腰三角形的两个内角之差为30°，
∴设较小的内角是x，则较大的内角为x+30°．
当x是等腰三角形的底角时，x+x+x+30°=180°，解得x=50°，
∴此时各内角的度数分别为50°，50°，80°；
当x是等腰三角形的顶角时，x+x+30°+x+30°=180°，解得x=40°，
∴此时各内角的度数分别为40°，70°，70°．
点评 本题考查的是等腰三角形的性质，熟知等腰三角形的两个底角相等是解答此题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
15．正整数中，最小的偶数乘以最小的合数，积为（ ）
| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
12．
如图是一次函数y=kx+b的图象，当y＜2时，x的取值范围是（ ）
如图是一次函数y=kx+b的图象，当y＜2时，x的取值范围是（ ）| A． | x＜1 | B． | x＞1 | C． | x＜3 | D． | x＞3 |
19．
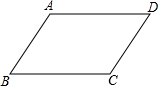对四边形ABCD加条件，使之成为平行四边形，下面的添加不正确的是（ ）
对四边形ABCD加条件，使之成为平行四边形，下面的添加不正确的是（ ）| A． | AB=CD，AB∥CD | B． | AB∥CD，AD=BC | C． | AB=CD，AD=BC | D． | AC与BD相互平分 |