题目内容
4.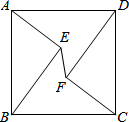 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD内的两点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD内的两点,且AE=FC=6,BE=DF=8,则EF的长为( )| A. | 2 | B. | 4 | C. | $\frac{4}{3}$$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 延长AE交DF于G,再根据全等三角形的判定得出△AGD与△ABE全等,得出AG=BE=8,由AE=6,得出EG=2,同理得出GF=2,再根据勾股定理得出EF的长.
解答 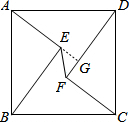 解:延长AE交DF于G,如图:
解:延长AE交DF于G,如图:
∵AB=10,AE=6,BE=8,
∴△ABE是直角三角形,
∴同理可得△DFC是直角三角形,
可得△AGD是直角三角形,
∴∠ABE+∠BAE=∠DAE+∠BAE,
∴∠GAD=∠EBA,
同理可得:∠ADG=∠BAE,
在△AGD和△BAE中,
$\left\{\begin{array}{l}{∠EAB=∠GDA}\\{AD=AB}\\{∠ABE=∠DAG}\end{array}\right.$,
∴△AGD≌△BAE(ASA),
∴AG=BE=8,DG=AE=6,
∴EG=2,
同理可得:GF=2,
∴EF=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
故选D.
点评 此题考查正方形的性质,关键是根据全等三角形的判定和性质得出EG=FG=2,再利用勾股定理计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.正整数中,最小的偶数乘以最小的合数,积为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
12. 如图是一次函数y=kx+b的图象,当y<2时,x的取值范围是( )
如图是一次函数y=kx+b的图象,当y<2时,x的取值范围是( )
 如图是一次函数y=kx+b的图象,当y<2时,x的取值范围是( )
如图是一次函数y=kx+b的图象,当y<2时,x的取值范围是( )| A. | x<1 | B. | x>1 | C. | x<3 | D. | x>3 |
19.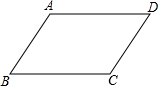 对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )
对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )
 对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )
对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )| A. | AB=CD,AB∥CD | B. | AB∥CD,AD=BC | C. | AB=CD,AD=BC | D. | AC与BD相互平分 |
13.为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.

捐款户数分组统计表
请结合以上信息解答下列问题.
(1)a=2,本次调查样本的容量是50;
(2)补全“捐款户数分组统计表和捐款户数分组统计图1”;
(3)若该社区有1500户住户,请根据以上信息,估计全社区捐款不少于150元的户数.

捐款户数分组统计表
| 组别 | 捐款额(x)元 | 户数 |
| A | 1≤x<50 | a |
| B | 50≤x<100 | 10 |
| C | 100≤x<150 | 20 |
| D | 150≤x<200 | 14 |
| E | x≥200 | 4 |
(1)a=2,本次调查样本的容量是50;
(2)补全“捐款户数分组统计表和捐款户数分组统计图1”;
(3)若该社区有1500户住户,请根据以上信息,估计全社区捐款不少于150元的户数.
 某农民带了若干千克玉米进城出卖,为了方便,他带了一些零用钱备用,他先按市场价出卖一些后,又降价卖,卖出玉米千克数x与他手中持有钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题.
某农民带了若干千克玉米进城出卖,为了方便,他带了一些零用钱备用,他先按市场价出卖一些后,又降价卖,卖出玉米千克数x与他手中持有钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题.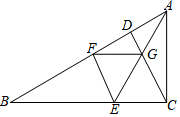 如图,在直角△ABC中,∠ACB=Rt∠,∠B=30°,CD为斜边AB上的高线,折叠△ABC使得AC落在AB上,点C与点F重合,展开的折痕AE交CD于点G,连接FG、EF.下列结论:①图中有6对全等三角形;②BC=6DG;③若将△EFG沿FG所在的直线折叠,则点E必在直线CD上;④AG=EF;⑤图中共有5个等腰直角三角形,其中正确的结论的个数是( )
如图,在直角△ABC中,∠ACB=Rt∠,∠B=30°,CD为斜边AB上的高线,折叠△ABC使得AC落在AB上,点C与点F重合,展开的折痕AE交CD于点G,连接FG、EF.下列结论:①图中有6对全等三角形;②BC=6DG;③若将△EFG沿FG所在的直线折叠,则点E必在直线CD上;④AG=EF;⑤图中共有5个等腰直角三角形,其中正确的结论的个数是( )