题目内容
20. 如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是( )
如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 以BC为轴作矩形ABCD的对称图形A′BCD′以及对称圆D′,连接AD′交BC于P,交⊙A、⊙D′于E、F′,连接PD,交⊙D于F,EF′就是PE+PF最小值;根据勾股定理求得AD′的长,即可求得PE+PF最小值.
解答  解:如图,以BC为轴作矩形ABCD的对称图形A′BCD′以及对称圆A′,连接A′D交BC于P,则DE′就是PE+PD最小值;
解:如图,以BC为轴作矩形ABCD的对称图形A′BCD′以及对称圆A′,连接A′D交BC于P,则DE′就是PE+PD最小值;
∵矩形ABCD中,AB=2,BC=3,圆A的半径为1,
∴A′D′=BC=3,AA′=2AB=4,AE=D′F′=1,
∴AD′=5,
EF′=5-2=3
∴PE+PF=PF′+PE=EF′=3,
故选B.
点评 本题考查了轴对称-最短路线问题,勾股定理的应用等,作出对称图形是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列说法正确的有( )
①有两边和一角对应相等的两个三角形全等;
②有一个角为100°,且腰长对应相等的两个等腰三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④三条边对应相等的两个三角形对应角也是相等的.
①有两边和一角对应相等的两个三角形全等;
②有一个角为100°,且腰长对应相等的两个等腰三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④三条边对应相等的两个三角形对应角也是相等的.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列说法:
①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③-$\sqrt{17}$是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③-$\sqrt{17}$是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
9.已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点M(-2,2),则k的值是( )
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
 如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1.
如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1. 如图,在Rt△OAB中,∠OAB=90°,点B的坐标为(4,2).
如图,在Rt△OAB中,∠OAB=90°,点B的坐标为(4,2).
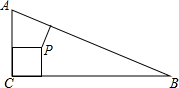 如图,在△ABC中,∠C=90°,两直角边AC=5,BC=12,在三角形内有一点P,它到各边的距离相等,则这个距离2.
如图,在△ABC中,∠C=90°,两直角边AC=5,BC=12,在三角形内有一点P,它到各边的距离相等,则这个距离2.