题目内容
15.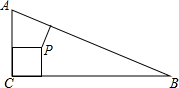 如图,在△ABC中,∠C=90°,两直角边AC=5,BC=12,在三角形内有一点P,它到各边的距离相等,则这个距离2.
如图,在△ABC中,∠C=90°,两直角边AC=5,BC=12,在三角形内有一点P,它到各边的距离相等,则这个距离2.
分析 连接PA、PB、PC,设点到各边的距离为x,根据勾股定理求出斜边长,根据三角形的面积公式计算即可.
解答 解: 连接PA、PB、PC,
连接PA、PB、PC,
设点到各边的距离为x,
∵∠C=90°,两直角边AC=5,BC=12,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
由题意得,$\frac{1}{2}$×AC×x+$\frac{1}{2}$×BC×x+$\frac{1}{2}$×AB×x=$\frac{1}{2}$×AC×BC,
解得,x=2,
故答案为:2.
点评 本题考查的是角平分线的性质,正确根据题意和三角形的面积公式列出方程是解题的关键.

练习册系列答案
相关题目
5.如图所示4个汉字中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知△ABC,以AB为直径的⊙O交AC于点F,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下四个结论:
如图,已知△ABC,以AB为直径的⊙O交AC于点F,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下四个结论: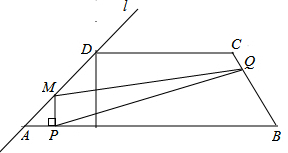
 如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是( )
如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是( ) 如图,从边长为4cm的正方体的一顶点处挖去一个边长为1cm的小正方体,则剩下的几何体的表面积为96cm2.
如图,从边长为4cm的正方体的一顶点处挖去一个边长为1cm的小正方体,则剩下的几何体的表面积为96cm2.