题目内容
16．
如图，点G为△ABC的重心，DE经过点G，DE∥AC，EF∥AB，如果DE的长是4，那么CF的长是2．
分析 连接BD并延长交AC于H，根据重心的性质得到$\frac{BG}{BH}$=$\frac{2}{3}$，根据相似三角形的性质求出AC，根据平行四边形的判定和性质求出AF，计算即可．
解答 解：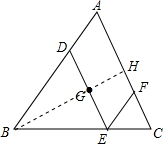
连接BD并延长交AC于H，
∵点G为△ABC的重心，
∴$\frac{BG}{BH}$=$\frac{2}{3}$，
∵DE∥AC，
∴△BDE∽△BAC，
∴$\frac{DE}{AC}$=$\frac{BG}{BH}$=$\frac{2}{3}$，又DE=4，
∴AC=6，
∵DE∥AC，EF∥AB，
∴四边形ADEF是平行四边形，
∴AF=DE=4，
∴CF=AC-AF=2，
故答案为：2．
点评 此题考查了重心的概念和性质：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．
练习册系列答案
相关题目
如图，⊙O是△ABC外接圆，∠A=45°，BD为⊙O的直径，BD=2，连结CD，求BC的长$\sqrt{2}$．
已知∠BOC=30°，OM平分∠AOC，ON平分∠BOC，
1．某校举行全体学生“汉字听写”比赛，每位学生听写汉字49个．随机抽取了部分学生的听写结果，绘制成如下的图表．
根据以上信息完成下列问题：
（1）统计表中的m=30，n=20，并补全条形统计图；
（2）求扇形统计图中“C组”所对应的圆心角的度数；
（3）已知该校共有2400名学生，如果听写正确的汉字的个数少于30个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
| 组别 | 正确字数x | 人数 |
| A | 0≤x＜10 | 10 |
| B | 10≤x＜20 | 15 |
| C | 20≤x＜30 | 25 |
| D | 30≤x＜40 | m |
| E | 40≤x＜50 | n |
（1）统计表中的m=30，n=20，并补全条形统计图；
（2）求扇形统计图中“C组”所对应的圆心角的度数；
（3）已知该校共有2400名学生，如果听写正确的汉字的个数少于30个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
如图，一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A（-2，m），B（5，-2）两点，与x轴交于C点，过A作AD⊥x轴于D．