题目内容
4. 如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.
如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.
分析 连接EF,先证明四边形ADFE是平行四边形,得出GE=GD,同理:HE=HC,证出GH是△EDC的中位线,由三角形中位线定理即可得出结论.
解答 证明:连接EF,如图所示:
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∵E,F分别为AB,CD的中点,
∴AE=$\frac{1}{2}$AB,DF=$\frac{1}{2}$DC,
∴AE=DF,
∴四边形ADFE是平行四边形,
∴GE=GD,
同理:HE=HC,
∴GH是△EDC的中位线,
∴GH=$\frac{1}{2}$DC.
点评 本题考查了平行四边形的性质与判定、三角形中位线定理;熟练掌握平行四边形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
14.若一批学生的年龄(单位:岁)分别是14,15,16,16,17,17,则这批学生年龄的中位数是( )
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
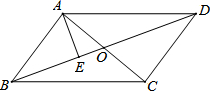 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.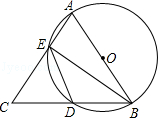 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.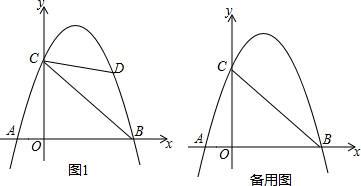
 如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0).
如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0).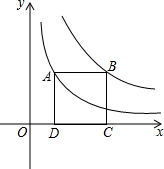 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{6}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD为正方形,则AB=2.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{6}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD为正方形,则AB=2.

 小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )
小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )