题目内容
19. 如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0).
如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0).(1)过点作DE⊥x轴,垂足为E,△OBC与△ECD全等吗?请说明理由;
(2)写出点D的坐标;
(3)用同样的方法求点A的坐标.
分析 (1)根据正方形性质和垂直得出∠DEC=∠BOC=∠BCD=90°,BC=CD,求出∠OBC=∠DCE,根据全等三角形的判定推出即可;
(2)根据全等三角形的性质得出OB=CE,OC=DE,求出DE=OC=4,CE=OB=3,求出OE=7,即可得出答案;
(3)过A作AF⊥y轴于F,同法求出△AFB≌△BOC,推出OB=AF,BF=OC,即可得出答案.
解答 解:(1)△OBC与△ECD全等,
理由是:∵DE⊥x轴,四边形ABCD是正方形,
∴∠DEC=∠BOC=∠BCD=90°,BC=CD,
∴∠OBC+∠OCB=90°,∠OCB+∠DCE=90°,
∴∠OBC=∠DCE,
在△BOC和△CED中,
$\left\{\begin{array}{l}{∠OBC=∠DCE}\\{∠BOC=∠DEC}\\{BC=DC}\end{array}\right.$,
∴△BOC≌△CED;
(2)∵△BOC≌△CED,
∴OB=CE,OC=DE,
∵点B(0,3),C(4,0),
∴OB=3,OC=4,
∴DE=OC=4,CE=OB=3,
∴OE=3+4=7,
∴点D的坐标是(7,4);
(3)如图,过A作AF⊥y轴于F,
∵AF⊥y轴,四边形ABCD是正方形,
∴∠AFB=∠BOC=∠ABC=90°,BC=AB,
∴∠FAB+∠FBA=90°,∠FBA+∠OBC=90°,
∴∠FAB=∠OBC,
在△AFB和△BOC中,
$\left\{\begin{array}{l}{∠FAB=∠OBC}\\{∠AFB=∠BOC}\\{AB=BC}\end{array}\right.$,
∴△AFB≌△BOC,
∴OB=AF,BF=OC,
∵点B(0,3),C(4,0),
∴OB=3,OC=4,
∴BF=OC=4,AF=OB=3,
∴OF=3+4=7,
∴点A的坐标是(4,7).
点评 本题考查了全等三角形的判定和性质,三角形的内角和定理,正方形的性质的应用,能推出两三角形全等是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

 阅读快车系列答案
阅读快车系列答案| 身高(厘米) | 159 | 160 | 162 | 165 | 167 | 168 |
| 人数 | 3 | 5 | 8 | 18 | 10 | 8 |
| A. | 159 | B. | 162 | C. | 165 | D. | 167 |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
 在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.
在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.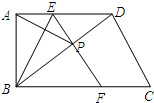 如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c. 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$.
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$. 如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.
如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.
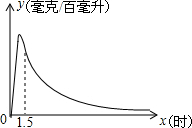 实验数据显示:一般成人喝半斤低度白酒后,其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系为:当0≤x≤1.5时,y与x成二次函数关系,即y=-200x2+400x;当x≥1.5时,y与x成反比例函数关系,即y=$\frac{k}{x}$.
实验数据显示:一般成人喝半斤低度白酒后,其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系为:当0≤x≤1.5时,y与x成二次函数关系,即y=-200x2+400x;当x≥1.5时,y与x成反比例函数关系,即y=$\frac{k}{x}$.