题目内容
9.在平行四边形ABCD中,点E是BC边的中点,延长AE交DC的延长线于点F,连接AC、BF.(1)如图1,求证:四边形ABFC是平行四边形;
(2)如图2,连接DE交AC于点G,若DE⊥AF,∠ADE=30°,判断四边形ABFC的形状,并说明理由.

分析 (1)欲证明四边形ABFC是平行四边形,只需推知AE=EF即可;
(2)首先推知四边形ABFC为平行四边形,证出BC=AF,即可得出四边形ABFC是矩形.
解答  (1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,
(1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,
∴∠BAE=∠EFC,
∵E为BC的中点,
∴BE=EC,
在△ABE和△FCE中,$\left\{\begin{array}{l}{∠BAE=∠EFC}\\{∠AEB=∠FEC}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△FCE(AAS),
∴AE=EF.
又∵BE=CE,
∴四边形ABFC是平行四边形;
(2)结论:四边形ABFC是矩形.
理由:∵DE⊥AF,AE=EF,
∴DE是AF的垂直平分线,
∴AD=DE,
∴∠ADF=2∠ADE=60°,
∴△AFE是等边三角形,
∴AF=AD,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴BC=AF,
∴平行四边形ABFC是矩形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质、矩形的判定.本题综合性强,难度适中,证明三角形全等和平行四边形是解决问题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
17. 如图,表示下列某个不等式的解集,其中正确的是( )
如图,表示下列某个不等式的解集,其中正确的是( )
 如图,表示下列某个不等式的解集,其中正确的是( )
如图,表示下列某个不等式的解集,其中正确的是( )| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤-2 |
14.菱形具有而矩形不一定具有的性质是( )
| A. | 对角相等 | B. | 每条对角线平分一组对角 | ||
| C. | 对角线互相平分 | D. | 对边平行且相等 |
 如图,在△ABC中,AB=AC.D 是BC上一点,且AD=BD.将△ABD绕点A逆时针旋转得到△ACE.
如图,在△ABC中,AB=AC.D 是BC上一点,且AD=BD.将△ABD绕点A逆时针旋转得到△ACE. 如图,已知EF∥AB,∠1=∠B,求证:∠EDC=∠DCB.
如图,已知EF∥AB,∠1=∠B,求证:∠EDC=∠DCB. 如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.
如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.
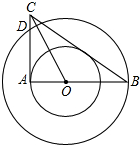 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.