题目内容
1.将一张长与宽之比为$\sqrt{2}$的矩形纸片ABCD进行如下操作:对折并沿折痕剪开,发现每一次所得到的两个矩形纸片长与宽之比都是$\sqrt{2}$(每一次的折痕如下图中的虚线所示).已知AB=1,则第3次操作后所得到的其中一个矩形纸片的周长是$\frac{{2+\sqrt{2}}}{2}$;第2016次操作后所得到的其中一个矩形纸片的周长是$\frac{{1+\sqrt{2}}}{{{2^{1007}}}}$.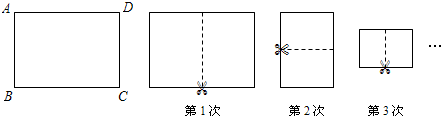
分析 先求出矩形纸片的长,再根据矩形的周长公式分别求出每一次对折后的周长,进而得出变化规律求出即可.
解答 解:1×$\sqrt{2}$=$\sqrt{2}$,
对开次数:
第一次,周长为:2(1+$\frac{1}{2}$$\sqrt{2}$)=2+$\sqrt{2}$,
第二次,周长为:2($\frac{1}{2}$+$\frac{1}{2}$$\sqrt{2}$)=1+$\sqrt{2}$,
第三次,周长为:2($\frac{1}{2}$+$\frac{1}{4}$$\sqrt{2}$)=$\frac{2+\sqrt{2}}{2}$,
第四次,周长为:2($\frac{1}{4}$+$\frac{1}{4}$$\sqrt{2}$)=$\frac{1+\sqrt{2}}{2}$,
第五次,周长为:2($\frac{1}{4}$+$\frac{1}{8}$$\sqrt{2}$)=$\frac{2+\sqrt{2}}{4}$,
…
∴第3次操作后所得到的其中一个矩形纸片的周长是$\frac{2+\sqrt{2}}{2}$,
第2016次对开后所得标准纸的周长为$\frac{{1+\sqrt{2}}}{{{2^{1007}}}}$.
故答案为:$\frac{2+\sqrt{2}}{2}$;$\frac{{1+\sqrt{2}}}{{{2^{1007}}}}$.
点评 此题主要考查了翻折变换性质以及规律性问题应用,根据已知得出对开后所得标准纸的周长变化规律是解题关键.

练习册系列答案
相关题目
16.已知3x=8,3y=2,则3x+y的值是( )
| A. | 4 | B. | 6 | C. | 10 | D. | 16 |
6.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a,b的值分别为( )

| A. | 9,10 | B. | 9,91 | C. | 10,91 | D. | 10,110 |
13.下列计算中,正确的是( )
| A. | 2a3(-a2)=-2a5 | B. | (a-b)2=a2-b2 | C. | (-a)5÷(-a)2=a3 | D. | (-3)-1=3 |
 你知道古代数学家怎样解一元二次方程吗?以x2-2x-3=0为例,大致过程如下:
你知道古代数学家怎样解一元二次方程吗?以x2-2x-3=0为例,大致过程如下: