题目内容
2.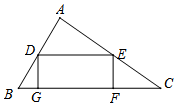 在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.
在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.
分析 如图,作AN⊥BC于N,交DE于M.首先求出AN,与DE∥BC,推出△ADE∽△ABC,推出$\frac{DE}{BC}$=$\frac{AM}{AN}$,可得$\frac{km}{6}$=$\frac{2-m}{2}$,推出m=$\frac{6}{3+k}$,由此即可解决问题.
解答 解:如图,作AN⊥BC于N,交DE于M.
∵S△ABC=$\frac{1}{2}$×BC×AN,
∴$\frac{1}{2}$×6×AN=6,
∴AN=2,设EF=m,则DE=km,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AM}{AN}$,
∴$\frac{km}{6}$=$\frac{2-m}{2}$,
∴m=$\frac{6}{3+k}$,
∴DE=$\frac{6k}{3+k}$,
∴四边形DEFG的面积=$\frac{6}{3+k}$•$\frac{6k}{3+k}$=$\frac{36k}{(3+k)^{2}}$.
点评 本题考查相似三角形的判定和性质、矩形的性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
12.据合肥市旅游局统计显示,2017年春节7天长假,合肥的景区、景点以及农家乐接待游客数目共达到265万人次,旅游总收入达到14.3亿元,其中14.3亿元用科学记数法表示是( )
| A. | 14.3×108元 | B. | 1.43×108元 | C. | 1.43×109元 | D. | 14.3×109元 |
13.数值0.0000105用科学记数法表示为( )
| A. | 1.05×104 | B. | 0.105×10-4 | C. | 1.05×10-5 | D. | 1.05×10-7 |
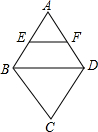 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=3,则菱形ABCD的边长是6.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=3,则菱形ABCD的边长是6.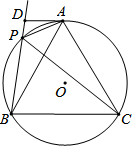 如图,⊙O是等边三角形ABC的外接圆,P是⊙O上一点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段AB的长是2+2$\sqrt{13}$.
如图,⊙O是等边三角形ABC的外接圆,P是⊙O上一点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段AB的长是2+2$\sqrt{13}$.