题目内容
（-a-b）（a-b）等于_______；
b2-a2
【解析】根据平方差公式可得：（-a-b）（a-b）=b2-a2.
练习册系列答案
相关题目
等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（ ）
A. 60° B. 120° C. 60°或150° D. 60°或120°
D
【解析】试题分析：等腰三角形的高相对于三角形有三种位置关系，三角形内部，三角形的外部，三角形的边上．根据条件可知第三种高在三角形的边上这种情况不成了，因而应分两种情况进行讨论．
【解析】
当高在三角形内部时（如图1），顶角是60°；
当高在三角形外部时（如图2），顶角是120°．
故选D． （3a-b）（3a+b）-（a+b）2
8a2-2b2-2ab
【解析】试题分析：先根据平方差公式与完全平方公式分别计算，再合并同类项即可.
试题解析：
（3a-b）（3a+b）-（a+b）2=9a2-b2-a2-b2-2ab=8a2-2b2-2ab. （2x-y 2 ） 2 等于（ ）
A. 2x2-4xy 2+y4 B. 4x2-2xy 2+y4 C. 4x2-4xy 2+y4 D. 4x2-xy 2+y4
C
【解析】根据完全平方公式可得：（2x-y 2 ） 2 =4x2-4xy 2+y4 ，故选C. （a-b）（a+b）-（a2+b2）
-2b2
【解析】试题分析：先根据平方差公式计算，再合并同类项即可.
试题解析：
（a-b）（a+b）-（a2+b2）=a2-b2-a2-b2=-2b2. [（c2)2+（a2)2][（c2)2-（a2)2]等于（ ）
A. c -a2 B. 4c2 -a8 C. c8 -a8 D. c2 -a4
C
【解析】根据平方差公式和幂的乘方法则可得：[（c2)2+（a2)2][（c2)2-（a2)2]= =c8 -a8，故选C. 下面计算正确的是（ ）
A. (a+b)(a-b)=2a+2b B. b5 + b5 = b10 C. x5·x5 = x25 D. (y-z)(y+z)=y2-z2
D
【解析】选项A，原式=a2-b2 ；选项 B，原式=2b5；选项C，原式=x10 ；选项D，原式= y2-z2.故选D. 若等腰三角形的一个外角为40°，则它的顶角的度数为_____.
140°
【解析】由等腰三角形的一个外角为40°，可得这个等腰三角形的一个内角为140°，根据三角形的内角和定理可得这个角为等腰三角形的顶角，即这个等腰三角形顶角的度数为140°. 分式有意义、无意义、值为0的条件：对于分式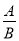
，(1)当_____时，分式有意义；(2)当_____时，分式无意义；(3)当A＝0且______时，分式的值为0.
B≠0 B＝0 B≠0
【解析】根据分母不等于0时分式有意义；分母等于0时分式无意义；分母不等于0且分子得0时，分式值为0即可得出答案.
【解析】
（1）当B≠0时，分式有意义；
（2）当B＝0时，分式无意义；
（3）当A＝0且B≠0时，分式的值为0.
故答案为：B≠0；B＝0；B≠0.