题目内容
13.感知:如图1,在正方形ABCD中,对角线AC,BD交于点O,G在OA上,CF⊥BG交OB于E,垂足为F,则△BOG≌△COE.探究:在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=$\frac{1}{2}$∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.求PE与BF的数量关系.并结合图2说明理由.
应用:把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=30°,求$\frac{BF}{PE}$=$\frac{\sqrt{3}}{6}$.(结果保留根号)

分析 探究:首先过P作PM∥AC交BG于M,交BO于N,易证得△BMN≌△PEN(ASA),△BPF≌△MPF(ASA),即可得BM=PE,BF=$\frac{1}{2}$BM.则可求得$\frac{BF}{PE}$的值;
应用:首先过P作PM∥AC交BG于点M,交BO于点N,由(1)同理可得:BF=$\frac{1}{2}$BM,∠MBN=∠EPN,继而可证得:△BMN∽△PEN,然后由相似三角形的对应边成比例,求得$\frac{BF}{PE}$的值.
解答 解:探究:如图2,过P作PM∥AC交BG于M,交BO于N,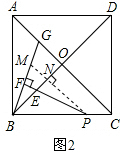
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB,
∴NB=NP,
∵∠MBN=90°-∠BMN,∠NPE=90°-∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中,
$\left\{\begin{array}{l}{∠MBN=∠NPE}\\{NB=NP}\\{∠MNB=∠PNE=90°}\end{array}\right.$,
∴△BMN≌△PEN(ASA),
∴BM=PE,
∵∠BPE=$\frac{1}{2}$∠ACB,∠BPN=∠ACB,
∴∠BPF=∠MPF,
∵PF⊥BM,
∴∠BFP=∠MFP=90°,
在△BPF和△MPF中,
$\left\{\begin{array}{l}{∠BPF=∠MPF}\\{PF=PF}\\{∠PFB=∠PFM}\end{array}\right.$,
∴△BPF≌△MPF(ASA),
∴BF=MF,
即BF=$\frac{1}{2}$BM,
∴BF=$\frac{1}{2}$PE,
即$\frac{BF}{PE}$=$\frac{1}{2}$;
应用:如图3,过P作PM∥AC交BG于点M,交BO于点N,
∴∠BPN=∠ACB=30°,∠PNE=∠BOC=90°,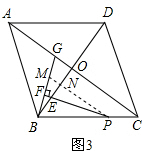
由探究:同理可得:BF=$\frac{1}{2}$BM,∠MBN=∠EPN,
∵∠BNM=∠PNE=90°,
∴△BMN∽△PEN,
∴$\frac{BM}{PE}=\frac{BN}{PN}$,
在Rt△BNP中,tan30°=$\frac{BN}{PN}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{BM}{PE}$=$\frac{\sqrt{3}}{3}$,
即$\frac{2BF}{PE}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{BF}{PE}=\frac{\sqrt{3}}{6}$,
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题主要考查了正方形的性质、菱形的性质、相似三角形的判定与性质、全等三角形的判定与性质以及三角函数的定义等知识,注意准确作出辅助线,注意数形结合思想的应用是解此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 菱形的对角线互相垂直平分 | |
| B. | 有一斜边与一直角边对应相等的两直角三角形全等 | |
| C. | 有一组邻边相等且垂直的平行四边形是正方形 | |
| D. | 对角线相等的四边形是矩形 |
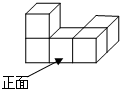 如图是五个相同的正方体组成的一个几何体,则其俯视图是( )
如图是五个相同的正方体组成的一个几何体,则其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
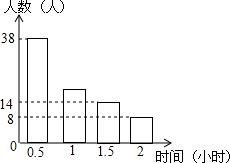 随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:
随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:| 上微信的时间(小时) | 频数(人数) | 频率 |
| 0.5 | 38 | a |
| 1 | b | 0.25 |
| 1.5 | 14 | c |
| 2 | 8 | 0.1 |
(1)结合统计图表,统计表中a=0.475,b=20;
(2)所抽查的学生上微信的平均时间为0.9875小时;
(3)若该校有640名学生,请你估计该校每天上微信的时间不少于1小时的学生有多少人?
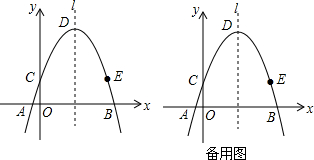
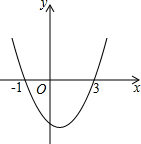 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论不正确的是( )| A. | b2-4ac>0 | B. | b+2a=0 | C. | abc>0 | D. | 8a+c<0 |
 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )| A. | 5cm | B. | 10cm | C. | 20cm | D. | 5πcm |