题目内容
19.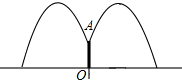 如图,公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,OA=1.5m,水流从A处喷出,在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(精确到0.1m)
如图,公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,OA=1.5m,水流从A处喷出,在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(精确到0.1m)
分析 建立直角坐标系,设过点A、C、B的抛物线解析式为y=ax2+bx+c,根据点A、C的坐标以及抛物线的对称轴为x=1即可列出关于a、b、c的三元一次方程组,解方程求出a、b、c的值,再利用二次函数图象上点的坐标特征求出点B的坐标即可得出结论.
解答 解:以O为原点,地面为x轴,喷水柱OA为y轴建议直角坐标系,设水落在x轴正半轴的位置为点B,水流最高点有一点味C,如图所示.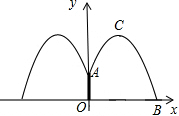
∵OA=1.5m,水流在离OA距离为1m处达到距水面最大高度2.25m,
∴A(0,1.5),C(1,2.25).
设过点A、C、B的抛物线解析式为y=ax2+bx+c,
将点A(0,1.5)、C(1,2.25)代入y=ax2+bx+c中,
$\left\{\begin{array}{l}{c=1.5}\\{-\frac{b}{2a}=1}\\{a+b+c=2.25}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-0.75}\\{b=1.5}\\{c=1.5}\end{array}\right.$,
∴过点A、C、B的抛物线解析式为y=-0.75x2+1.5x+1.5.
当y=0时,则有-0.75x2+1.5x+1.5=0,
解得:x=1+$\sqrt{3}$≈2.8或x=1-$\sqrt{3}$(舍去),
∴水池的半径至少要2.8米,才能使喷出的水流不致落到池外.
点评 本题考查了待定系数法求函数解析式,解题的关键是建立合适的直角坐标系,根据点的坐标利用待定系数法求出函数解析式.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
6.计算:$\frac{1}{2}$×($\sqrt{3}-1$)2-($\sqrt{2}$+1)($\sqrt{2}-1$)+$\sqrt{3}$-($\frac{\sqrt{2}}{2}$)-1.
7.下列方程中,是二元二次方程的为( )
| A. | 2x2+3x-4=0 | B. | y2+2x=0 | C. | x2+$\sqrt{3-y}$-7=0 | D. | y2+$\frac{1}{x-3}$=0 |
14.下列说法正确的是( )
| A. | 两条对角线互相垂直且相等的四边形是正方形 | |
| B. | 两条对角线互相垂直的四边形是菱形 | |
| C. | 两条对角线相等的四边形是矩形 | |
| D. | 两条对角线互相平分的四边形是平行四边形 |
4.下列各组式子中,是同类项是( )
| A. | $\frac{2}{3}$xyz与$\frac{2}{3}$xy | B. | $\frac{1}{x}$与2x | C. | -0.5x3y2与2x2y3 | D. | 5m2n与-2nm2 |