题目内容
13. (1)计算:($\frac{2}{3}$$\sqrt{3}$-$\sqrt{12}$)÷$\sqrt{3}$
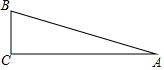
(1)计算:($\frac{2}{3}$$\sqrt{3}$-$\sqrt{12}$)÷$\sqrt{3}$(2)如图,Rt△ABC中,∠C=90°,AC=$\sqrt{3}$+$\sqrt{2}$,BC=$\sqrt{3}$-$\sqrt{2}$,求Rt△ABC的面积和斜边AB的长.
分析 (1)首先化简二次根式进而利用二次根式除法运算法则求出答案;
(2)直接利用直角三角形的性质分析得出答案.
解答 解:(1)($\frac{2}{3}$$\sqrt{3}$-$\sqrt{12}$)÷$\sqrt{3}$
=($\frac{2}{3}$$\sqrt{3}$-2$\sqrt{3}$)÷$\sqrt{3}$
=-$\frac{4}{3}$$\sqrt{3}$$÷\sqrt{3}$
=-$\frac{4}{3}$;
(2)∵AC=$\sqrt{3}$+$\sqrt{2}$,BC=$\sqrt{3}$-$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)
=$\frac{1}{2}$;
∵AB2=AC2+BC2=($\sqrt{3}$+$\sqrt{2}$)2+($\sqrt{3}$-$\sqrt{2}$)2=10,
∴AB=$\sqrt{10}$.
点评 此题主要考查了二次根式的应用以及二次根式的混合运算,正确掌握运算法则是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.计算(-a+2b)2-(-a-2b)2的结果是( )
| A. | -8ab | B. | -4ab | C. | 8ab | D. | 4ab |
1.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行;(2)过一点有且只有一条直线与已知直线垂直;(3)在同一平面内,两条直线的位置关系只有相交,平行两种;(4)不相交的两条直线叫做平行线.
(1)过一点有且只有一条直线与已知直线平行;(2)过一点有且只有一条直线与已知直线垂直;(3)在同一平面内,两条直线的位置关系只有相交,平行两种;(4)不相交的两条直线叫做平行线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.如果∠A和∠B的两边分别平行,∠A=60°,那么∠B是( )
| A. | 60° | B. | 30°或120° | C. | 120° | D. | 60°或120° |
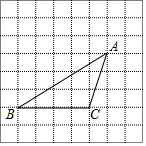 如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.
如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.