题目内容
1. 如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,当点D从点A运动到点B时,线段EF的最小值是5$\sqrt{3}$.
如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,当点D从点A运动到点B时,线段EF的最小值是5$\sqrt{3}$.
分析 连接CD,设ED交AC于点G,则点G为ED中点,可证得AC∥DF,得出C为EF中点,即EF=2CD,当CD⊥AB是有最小值,可求得EF的最小值.
解答  解:连接CD,设AC于点DE交于点G,则EG=DG,且ED⊥AC,
解:连接CD,设AC于点DE交于点G,则EG=DG,且ED⊥AC,
∵DF⊥DE,
∴∠EGC=∠EDF=90°,
∴AC∥DF,且G为ED中点,
∴EC=FC,即EF=2CD,
∴当线段EF最小时,线段CD也最小,
根据垂直线段最短的性质,当CD⊥AD时线段CD最小,
∵AB是半圆O 的直径,
∴∠ACB=90°,
∵AB=10,∠CBA=30°,
∴AC=5,BC=5$\sqrt{3}$,
当CD⊥AD时,CD=$\frac{1}{2}$BC=$\frac{5}{2}$$\sqrt{3}$,此时EF=2CD=5$\sqrt{3}$、
故答案为:5$\sqrt{3}$.
点评 本题主要考查圆周角定理及轴对称的性质、勾股定理等知识的综合应用,题中把EF的值转化成CD的值是解答此题的关键.

练习册系列答案
相关题目
8.已知xy>0,化简二次根式x$\sqrt{\frac{-y}{{x}^{2}}}$的正确结果为( )
| A. | $\sqrt{y}$ | B. | $\sqrt{-y}$ | C. | -$\sqrt{y}$ | D. | -$\sqrt{-y}$ |
15.计算(-12)-(-3)+(-10)-(-9)-$\frac{1}{3}$的结果是( )
| A. | $-\frac{25}{3}$ | B. | $-\frac{43}{3}$ | C. | $-\frac{49}{3}$ | D. | $-\frac{31}{3}$ |
6.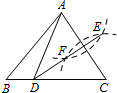 如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )
如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )
 如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )
如图,在△ABC中,分别以点A、C为圆心,以大于$\frac{AC}{2}$长为半径作圆弧,两弧分别相交于点E、F,连结EF并延长交边BC于点D,连结AD.若AB=6,BC=8,则△ABD的周长为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
10.三角形中,两边长分别为4和5,第三边上的高为3,则此三角形面积为( )
| A. | $\frac{15}{2}$ | B. | $\frac{3}{2}$($\sqrt{7}$+4) | C. | 6 | D. | $\frac{3}{2}$(4±$\sqrt{7}$) |

 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是( )
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是( ) 已知⊙O的半径为r,作⊙O的内接正方形ABCD.
已知⊙O的半径为r,作⊙O的内接正方形ABCD.