题目内容
6. 如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,∠P=60°,⊙O的半径为1,则劣弧$\widehat{AB}$的长为$\frac{2π}{3}$.
如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,∠P=60°,⊙O的半径为1,则劣弧$\widehat{AB}$的长为$\frac{2π}{3}$.
分析 欲求$\widehat{AB}$的弧长,只需求得该弧所对的圆心角∠AOB的度数.
解答 解:∵PA、PB是⊙O的切线,切点分别是A、B,
∴∠OAP=∠OBP=90°,
∵∠P=60°,
∴∠AOB=120°
∵OA=6,
∴$\widehat{AB}$=$\frac{120π×1}{180}$=$\frac{2π}{3}$,
故答案为$\frac{2π}{3}$.
点评 本题考查了切线的性质,切线长定理的运用,弧长公式的运用.注意四边形的内角和的运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
11. 如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
 如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )
如图,已知△ABC中,点D在AB上,且CD=AD=BD,点F在BC上,过D作DE⊥DF交AC于E,过F作FG⊥AB于G,以下结论:①△ABC为直角三角形,②BF2+DG2=DF2+BG2,③AE2+BF2=CE2+CF2,④AG2=AC2+BG2,其中结论正确的序号是( )| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②③④ |
18.有一列数a,b,c,d,…,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差.若第一个数a等于2,则第2014个数等于( )
| A. | 2014 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |

 2003~2005年某市的财政收入情况如图所示.根据图中的信息,解答下列问题:
2003~2005年某市的财政收入情况如图所示.根据图中的信息,解答下列问题: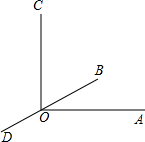 如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.
如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.