题目内容
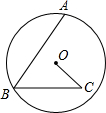 如图,AB是⊙O的弦,点C在⊙O内,∠ABC=∠OCB=60°,若BC=6,OC=4,求弦AB和⊙O半径的长.
如图,AB是⊙O的弦,点C在⊙O内,∠ABC=∠OCB=60°,若BC=6,OC=4,求弦AB和⊙O半径的长.考点:垂径定理,等边三角形的判定与性质
专题:
分析:延长CO交AB于E,过O作OQ⊥AB于Q,连接OB,得出等边三角形EBC,求出OE,解直角三角形求出QE,OQ,根据勾股定理求出OB,即可得出答案.
解答:解: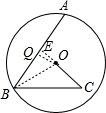
延长CO交AB于E,过O作OQ⊥AB于Q,连接OB,
则由垂径定理得:AB=2BQ,
∵∠ABC=∠OCB=60°,
∴BE=CE,
∵BC=6,
∴三角形EBC是等边三角形,边长为6,
∴OE=6-4=2,BE=6,∠BEC=60°,
∵OQ⊥AB,
∴∠EQO=90°,
∴∠QOE=30°,
∴QE=
OE=1,OQ=
,
在Rt△OBQ中,BQ=6-1=5,OQ=
,由勾股定理得:OB=
=2
,
即AB=2BQ=10,⊙O半径的长是2
.

延长CO交AB于E,过O作OQ⊥AB于Q,连接OB,
则由垂径定理得:AB=2BQ,
∵∠ABC=∠OCB=60°,
∴BE=CE,
∵BC=6,
∴三角形EBC是等边三角形,边长为6,
∴OE=6-4=2,BE=6,∠BEC=60°,
∵OQ⊥AB,
∴∠EQO=90°,
∴∠QOE=30°,
∴QE=
| 1 |
| 2 |
| 3 |
在Rt△OBQ中,BQ=6-1=5,OQ=
| 3 |
52+(
|
| 7 |
即AB=2BQ=10,⊙O半径的长是2
| 7 |
点评:本题考查了等边三角形的性质和判定,垂径定理,解直角三角形,勾股定理的应用,主要考查学生的推理和计算能力.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 有理数a、b在数轴上的位置如图所示,则化简|b-a|-b的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|b-a|-b的结果为( )| A、a-2b | B、-a |
| C、-2b-a | D、2b-a |
 如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.
如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.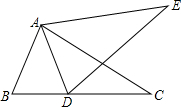 如图,D是BC上一点,AB=AD,BC=DE.△ABC≌△ADE,求证:∠CDE=∠BAD.
如图,D是BC上一点,AB=AD,BC=DE.△ABC≌△ADE,求证:∠CDE=∠BAD.