题目内容
 函数y=ax2与直线y=-2x-4交于点(2,b).
函数y=ax2与直线y=-2x-4交于点(2,b).(1)求a和b的值;
(2)写出抛物线的顶点坐标和对称轴;画出此二次函数的图象;
(3)函数y=ax2,当x取何值时,y随x的增大而增大?
| … | … | ||||||||
| … | … |
考点:二次函数图象上点的坐标特征,一次函数图象上点的坐标特征,二次函数的图象,二次函数的性质
专题:计算题
分析:(1)先把(2,b)代入y=-2x-4可求出b的值,从而得到交点坐标,然后把交点坐标代入y=ax2可求出a的值;
(2)根据二次函数的性质易得抛物线的顶点坐标和对称轴,然后利用列表、描点和连线画二次函数图象;
(3)根据二次函图象的性质求解.
(2)根据二次函数的性质易得抛物线的顶点坐标和对称轴,然后利用列表、描点和连线画二次函数图象;
(3)根据二次函图象的性质求解.
解答:解:(1)把(2,b)代入y=-2x-4得b=-4-4=-8,
把(2,-8)代入y=ax2得4a=-8,解得a=-2;
(2)抛物线y=-2x2的顶点坐标为(0,0),对称轴为y轴,
列表:
描点,连线,如图:
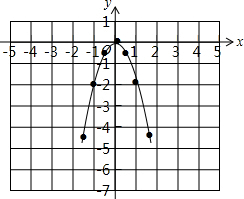
(3)当x<0时,y随x的增大而增大.
把(2,-8)代入y=ax2得4a=-8,解得a=-2;
(2)抛物线y=-2x2的顶点坐标为(0,0),对称轴为y轴,
列表:
| x | … | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | … |
| y | … | -4.5 | -2 | -0.5 | 0 | -0.5 | -2 | -4.5 | … |

(3)当x<0时,y随x的增大而增大.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数图象与性质.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
若抛物线y=ax2+bx+c的对称轴是x=-2,则
等于( )
| a |
| b |
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
 如图,已知点A、D、C、F在同一条直线上,AB=DE,∠B=∠E,要使△ABC≌△DEF,还需要添加一个条件是
如图,已知点A、D、C、F在同一条直线上,AB=DE,∠B=∠E,要使△ABC≌△DEF,还需要添加一个条件是 如图,将一副直角三角板放在一起,使直角顶点重合于点O.
如图,将一副直角三角板放在一起,使直角顶点重合于点O.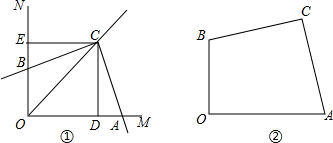
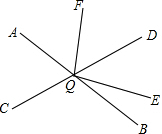 如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.
如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数. 如图,在△ABC中,∠B=2∠A,CD⊥AB于D,E为AB的中点,求证:DE=
如图,在△ABC中,∠B=2∠A,CD⊥AB于D,E为AB的中点,求证:DE=