题目内容
7.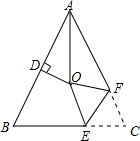 如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为128度.
如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为128度.
分析 先作辅助线,然后根据等腰三角形的性质和翻折变化的相关知识,可以求得∠OEC的度数,本题得以解决.
解答  解:连接OB、OC,
解:连接OB、OC,
∵AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,
∴点O是△ABC的外心,∠BAO=∠CAO=32°,∠ABC=∠ACB=58°,
∴OA=OB=OC,
∴∠OAB=∠OBA=32°,
∴∠OBC=∠OCB=26°,
∵∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴EC=EO,
∴∠EOC=∠ECO=26°,
∴∠OEC=180°-26°-26°=128°,
故答案为:128.
点评 本题考查翻折变化、等腰三角形的性质、线段的垂直平分线,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
18.一扇形的半径等于已知圆的半径的2倍,且它的面积等于该圆的面积,则这一扇形的圆心角为( )
| A. | 20° | B. | 120° | C. | 100° | D. | 90° |
2.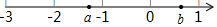 若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )
若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )
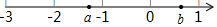 若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )
若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )| A. | |a|>|b| | B. | -2<a<-1,0<b<1 | C. | a+b<0 | D. | a>-1,0<b<1 |
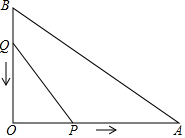 如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么:
如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么: 已知△ABC中,∠BAC=130°,BC=26,AB、AC的垂直平分线分别交BC于E、F,与AB、AC分别交于点D、G.求:
已知△ABC中,∠BAC=130°,BC=26,AB、AC的垂直平分线分别交BC于E、F,与AB、AC分别交于点D、G.求: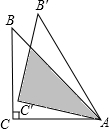 如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.
如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.