题目内容
15.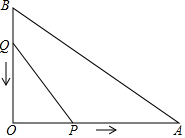 如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么:
如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么:(1)点Q运动多少秒时,△OPQ的面积为5cm2;
(2)当x为何值时,以P、O、Q为顶点的三角形与△AOB相似?
分析 (1)先根据勾股定理求出BO的长,再用x表示出OQ及OP的长,根据三角形的面积公式即可得出x的值;
(2)分△OPQ∽△OAB与△OPQ∽△OBA两种情况进行分类讨论.
解答 解:(1)∵∠AOB=90°,
∴BO2=AB2-AO2,
∴BO=6,
在Rt△OPQ中,OQ=6-x,OP=2x,
∵△OPQ的面积为5cm2;
∴$\frac{1}{2}$OQ•OP=5,即$\frac{1}{2}$(6-x)•2x=5,解得x1=1,x2=5;
(2)当△OPQ∽△OAB时,$\frac{OP}{OA}$=$\frac{OQ}{OB}$,即$\frac{2x}{12}$=$\frac{6-x}{6}$,解得x=3秒;
当△OPQ∽△OBA,$\frac{OP}{OB}$=$\frac{OQ}{OA}$,即$\frac{2x}{6}$=$\frac{6-x}{12}$,解得x=$\frac{6}{5}$秒.
综上所述,当x=3秒或$\frac{6}{5}$秒时,以P、O、Q为顶点的三角形与△AOB相似.
点评 本题考查的是相似三角形的判定,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
20.下列说法中,不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 绝对值最小的数是1 | ||
| C. | 一个有理数不是整数就是分数 | D. | 0的相反数是0 |
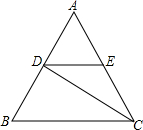 如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5.
如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5. 有理数a、b、c在数轴上的对应点如图所示,化简代数式|2a-b|+3|a+b|-|4c-a|=-4a-2b-4c.
有理数a、b、c在数轴上的对应点如图所示,化简代数式|2a-b|+3|a+b|-|4c-a|=-4a-2b-4c.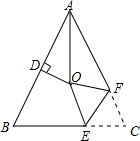 如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为128度.
如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为128度. 如图,该图形折叠成正方体后,与“沉”字相对的字是考.
如图,该图形折叠成正方体后,与“沉”字相对的字是考.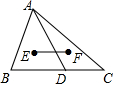 如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2.
如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2.