题目内容
19．已知5a-1的平方根是±3，b、c均为有理数，且b、c满足等式b+$\sqrt{3}$c+2$\sqrt{3}$=c2+5，求a+b+c的算术平方根．分析 根据平方根、算术平方根，即可解答．
解答 解：∵5a-1的平方根是±3，
∴5a-1=9
∴a=2，
∵b+$\sqrt{3}$c+2$\sqrt{3}$=c2+5，
∴c=-2，b=9，
∴a+b+c=2-2+9=9，
∴9的算术平方根是3．
点评 本题考查了实数，解决本题的关键是熟记平方根、算术平方根．
练习册系列答案
相关题目
9．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如表：
从表可知，
①抛物线与x轴的交点为（-2，0）和（3，0）；
②抛物线的对称轴是x=$\frac{1}{2}$；
③函数y=ax2+bx+c的最大值为$\frac{25}{4}$；
④x＜$\frac{1}{2}$，y随x增大而增大．
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的交点为（-2，0）和（3，0）；
②抛物线的对称轴是x=$\frac{1}{2}$；
③函数y=ax2+bx+c的最大值为$\frac{25}{4}$；
④x＜$\frac{1}{2}$，y随x增大而增大．
有理数a、b、c在数轴上的对应点如图所示，化简代数式|2a-b|+3|a+b|-|4c-a|=-4a-2b-4c．
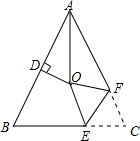如图，在△ABC中，AB=AC，∠BAC=64°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为128度．
在平面直角坐标系xOy中，己知A（-1，5），B（4，2），C（-1，0）三点．
如图，该图形折叠成正方体后，与“沉”字相对的字是考．