题目内容
16.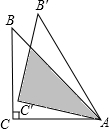 如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.
如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.
分析 AB与C′B′相交于点D,如图,根据等腰直角三角形的性质得AC=BC=6cm,∠CAB=45°,再根据旋转的性质得∠CAB=45°,∠CAC′=15°,则∠C′AD=30°,再利用含30度的直角三角形的三边的关系计算出C′D,然后根据三角形面积公式计算阴影部分的面积.
解答 解:AB与C′B′相交于点D,如图,
∵等腰Rt△ABC中,∠C=90°,BC=6cm,
∴AC=BC=6cm,∠CAB=45°,
∵△ABC绕点A顺时针旋转15°后得到△AB′C′,
∴∠CAB=45°,∠CAC′=15°,
∴∠C′AD=30°,
在Rt△AC′D中,C′D=$\frac{\sqrt{3}}{3}$AC′=$\frac{\sqrt{3}}{3}$×6=2$\sqrt{3}$,
∴阴影部分的面积=$\frac{1}{2}$×6×2$\sqrt{3}$=6$\sqrt{3}$.
故答案为$6\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列计算中正确的有( )个
①3x2+x2=4x4②3x2-x2=3③5a2b-6ba2=-a2b④-7a2=-14a.
①3x2+x2=4x4②3x2-x2=3③5a2b-6ba2=-a2b④-7a2=-14a.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
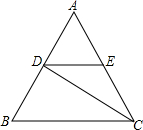 如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5.
如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5.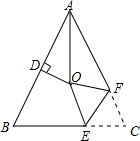 如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为128度.
如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为128度. 如图,该图形折叠成正方体后,与“沉”字相对的字是考.
如图,该图形折叠成正方体后,与“沉”字相对的字是考.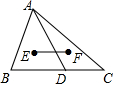 如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2.
如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2.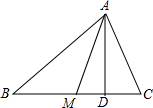 三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )
三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )