题目内容
10.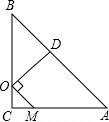 如图,在等腰Rt△ABC中,∠C=90°,AC=7.点O在BC上,且CO=1,点M是AC上一动点,连接OM,将线段OM绕点O逆时针旋转90°,得到线段OD,要使点D恰好落在AB上,CM的长度为5.
如图,在等腰Rt△ABC中,∠C=90°,AC=7.点O在BC上,且CO=1,点M是AC上一动点,连接OM,将线段OM绕点O逆时针旋转90°,得到线段OD,要使点D恰好落在AB上,CM的长度为5.
分析 如图,作辅助线;首先证明△DOE≌△OMC,得到OC=DE,CM=OE;其次证明BE=DE,求出OE,即可解决问题.
解答  解:如图,过点D作DE⊥OB于点E;
解:如图,过点D作DE⊥OB于点E;
∵∠DEO=∠DOM=∠C,
∴∠DOE+∠COM=∠COM+∠CMO,
∴∠DOE=∠OMC;
由题意得:OD=OM;
在△DOE与△OMC中,
$\left\{\begin{array}{l}{∠DOE=∠OMC}\\{∠DEO=∠OCM}\\{OD=OM}\end{array}\right.$,
∴△DOE≌△OMC(AAS),
∴DE=OC=1,CM=OE;
∵△ABC为等腰直角三角形,
∴∠B=45°,∠BDE=45°,
∴BE=DE=1,OE=7-1-1=5,
∴CM=OE=5,
故答案为5.
点评 该题主要考查了旋转变换的性质、等腰直角三角形的性质、全等三角形的判定等几何知识点及其应用问题;解题的方法是作辅助线,构造全等三角形;解题的关键是灵活运用旋转变换的性质等几何知识点来分析、判断、推理或解答.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
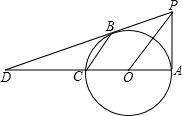 以AC=6为直径画一个圆,过点A作AP⊥AC,过点C作CB∥OP,直线PB与直线AC相交于点D.
以AC=6为直径画一个圆,过点A作AP⊥AC,过点C作CB∥OP,直线PB与直线AC相交于点D.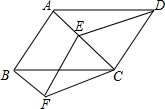 已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠DEC=∠ABC,且CD2=CE•CA.
已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠DEC=∠ABC,且CD2=CE•CA.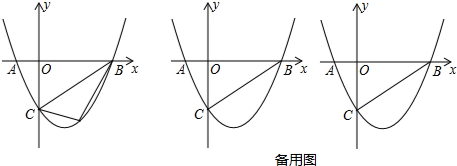
 如图,直线AB与x轴、y轴分别交于B、A两点,线段OA、OB的长是关于x的一元二次方程x2-14x+48=0的两个根(OA<OB)
如图,直线AB与x轴、y轴分别交于B、A两点,线段OA、OB的长是关于x的一元二次方程x2-14x+48=0的两个根(OA<OB)