题目内容
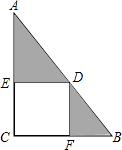 如图所示,在Rt△ABC中,∠C=90°,四边形ECFD为正方形,若AD=36,DB=4,求阴影部分的面积.
如图所示,在Rt△ABC中,∠C=90°,四边形ECFD为正方形,若AD=36,DB=4,求阴影部分的面积.考点:正方形的性质,旋转的性质
专题:
分析:把△ADE逆时针旋转90°,则DE和DF重合,此时△A′BD为直角三角形,且A′D=36,BD=4,可求得面积.
解答: 解:如图,把△ADE逆时针旋转90°,
解:如图,把△ADE逆时针旋转90°,
则△ADE≌△A′DF,
∴A′D=AD=36,∠A′DF=∠ADE,
∵∠ADE+∠BDF=90°,
∴∠A′DF+∠BDF=∠A′DB=90°,
∴S阴影=S△ADE+S△BDF=S△A′FD+S△BDF=S△A′DB=
A′D•BD=
×36×4=72.
 解:如图,把△ADE逆时针旋转90°,
解:如图,把△ADE逆时针旋转90°,则△ADE≌△A′DF,
∴A′D=AD=36,∠A′DF=∠ADE,
∵∠ADE+∠BDF=90°,
∴∠A′DF+∠BDF=∠A′DB=90°,
∴S阴影=S△ADE+S△BDF=S△A′FD+S△BDF=S△A′DB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查正方形的性质及旋转的性质,利用旋转把阴影部分转化成Rt△A′BD是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
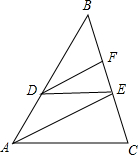 如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,
如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,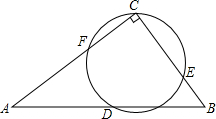 如图,Rt△ABC中,∠ACB=90°,AC=8,BC=6,D是AB中点,E是BC边上的动点,圆O过C、D、E三点,与AC边交于点F.
如图,Rt△ABC中,∠ACB=90°,AC=8,BC=6,D是AB中点,E是BC边上的动点,圆O过C、D、E三点,与AC边交于点F.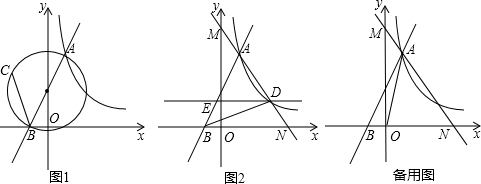
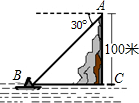 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,求船与观测者之间的水平距离(结果精确到0.1m).
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,求船与观测者之间的水平距离(结果精确到0.1m).