题目内容
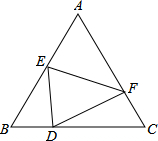 如图,已知等边△ABC,现将△ABC折叠,使A点落在BC边上D点,折痕为EF,求证:∠BED=∠FDC.
如图,已知等边△ABC,现将△ABC折叠,使A点落在BC边上D点,折痕为EF,求证:∠BED=∠FDC.考点:翻折变换(折叠问题),等边三角形的性质
专题:证明题
分析:由题意得:△AEF≌△DEF,故∠EDF=∠A=60°;由三角形的内角和定理及平角的知识问题即可解决.
解答: 解:由题意得:
解:由题意得:
△AEF≌△DEF,
∴∠EDF=∠A;
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∴∠EDF=60°;
∴∠BED+∠EDB=∠EDB+∠FDC=180°-60°=120°,
∴∠BED=∠FDC.
 解:由题意得:
解:由题意得:△AEF≌△DEF,
∴∠EDF=∠A;
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∴∠EDF=60°;
∴∠BED+∠EDB=∠EDB+∠FDC=180°-60°=120°,
∴∠BED=∠FDC.
点评:该命题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用全等三角形的性质、三角形的内角和定理等知识来解决问题.

练习册系列答案
相关题目
下列说法正确的是( )
A、在球的体积公V=
| ||||
| B、若变量x、y满足y2=x,则y是x的函数 | ||||
C、在圆锥的体积公式V=
| ||||
D、若变量x、y满足y=-
|
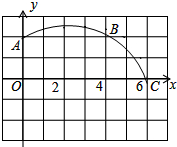 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题: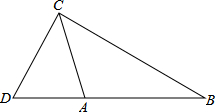 如图,在△ABC中,AC=5cm,BC=8cm,△ABC的面积为12cm,点D在BA延长线上,∠DCA=∠B.
如图,在△ABC中,AC=5cm,BC=8cm,△ABC的面积为12cm,点D在BA延长线上,∠DCA=∠B.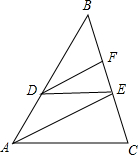 如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,
如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,