题目内容
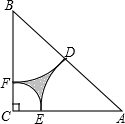 如图,在Rt△ABC中,∠C=90°,BC=AC=2cm,分别以A,C,B为圆心作弧,使
如图,在Rt△ABC中,∠C=90°,BC=AC=2cm,分别以A,C,B为圆心作弧,使 |
| DE |
 |
| EF |
 |
| FD |
(1)求
 |
| DE |
 |
| EF |
 |
| FD |
(2)求阴影部分的面积.
考点:相切两圆的性质,弧长的计算,扇形面积的计算
专题:
分析:(1)首先根据题意以及相切两圆的性质得出BD=AD=
cm,FC=EC=(2-
)cm,再利用弧长公式求出即可;
(2)利用(1)中所求,再利用扇形面积公式求出即可.
| 2 |
| 2 |
(2)利用(1)中所求,再利用扇形面积公式求出即可.
解答:解:(1)∵在Rt△ABC中,∠C=90°,BC=AC=2cm,
∴AB=2
cm,∠A=∠B=45°,
∵
、
、
所在的圆两两外切,BC=AC,
∴BD=AD=
cm,
则FC=EC=(2-
)cm,
∴
+
+
=
+
+
=π(cm);
(2)阴影部分的面积=
×2×2-
-
-
=(2-2π+
π)cm2.
∴AB=2
| 2 |
∵
 |
| DE |
 |
| EF |
 |
| FD |
∴BD=AD=
| 2 |
则FC=EC=(2-
| 2 |
∴
 |
| DE |
 |
| EF |
 |
| FD |
45π×
| ||
| 180 |
90π×(2-
| ||
| 180 |
45π×
| ||
| 180 |
(2)阴影部分的面积=
| 1 |
| 2 |
45π×(
| ||
| 360 |
45π×(
| ||
| 360 |
90π×(2-
| ||
| 360 |
| 2 |
点评:此题主要考查了相切两圆的性质以及弧长公式和扇形面积公式的应用,得出各扇形半径长是解题关键.

练习册系列答案
相关题目
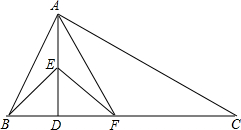 如图,在△ABC中,∠BAC=90°,AD是斜边BC上的高,∠ABD的平分线交AD于点E,∠CAD的平分线交CD于点F,连接EF.求证:EF∥AC.
如图,在△ABC中,∠BAC=90°,AD是斜边BC上的高,∠ABD的平分线交AD于点E,∠CAD的平分线交CD于点F,连接EF.求证:EF∥AC.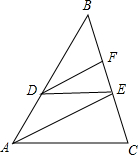 如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,
如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,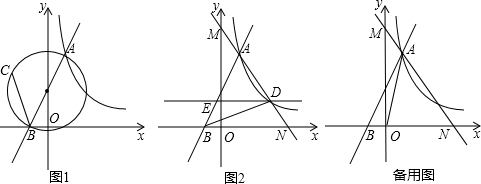
 如图所示,将△AOB绕着点O旋转180度得到△DOC.过点O的一条直线分别交BA、CD的延长线于点E、F.求证:AE=DF.
如图所示,将△AOB绕着点O旋转180度得到△DOC.过点O的一条直线分别交BA、CD的延长线于点E、F.求证:AE=DF.