题目内容
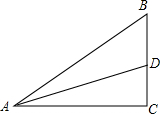 在Rt△ABC中,AD是角平分线,已知,AB=5,AC=4,BC=3,∠ACB=90°.
在Rt△ABC中,AD是角平分线,已知,AB=5,AC=4,BC=3,∠ACB=90°.(1)比较△ABD与△ACD的面积大小;
(2)求CD的长.
考点:角平分线的性质
专题:
分析:(1)过点D作DE⊥AB,由角平分线的性质可知DE=CD,故可得出两三角形面积的比;
(2)根据(1)中两三角形的面积比求出△ACD的面积,故可得出CD的长.
(2)根据(1)中两三角形的面积比求出△ACD的面积,故可得出CD的长.
解答: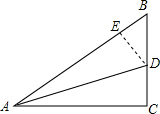 解:(1)过点D作DE⊥AB,
解:(1)过点D作DE⊥AB,
∵AD是角平分线,
∴CD=DE.
∵AB=5,AC=4,
∴
=
=
,即S△ABD>S△ACD;
(2)∵由(1)知,
=
=
,
∴S△ACD=
S△ABC=
×4×3=
,
∴
×4CD=
,解得CD=
.
 解:(1)过点D作DE⊥AB,
解:(1)过点D作DE⊥AB,∵AD是角平分线,
∴CD=DE.
∵AB=5,AC=4,
∴
| S△ABD |
| S△ACD |
| AB |
| AC |
| 5 |
| 4 |
(2)∵由(1)知,
| S△ABD |
| S△ACD |
| AB |
| AC |
| 5 |
| 4 |
∴S△ACD=
| 4 |
| 9 |
| 4 |
| 9 |
| 16 |
| 3 |
∴
| 1 |
| 2 |
| 16 |
| 3 |
| 8 |
| 3 |
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
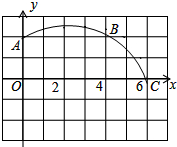 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题: 如图,已知∠AOB=90°,∠BOC比∠AOC大30°,OD是∠AOB的平分线,求∠COD的度数.
如图,已知∠AOB=90°,∠BOC比∠AOC大30°,OD是∠AOB的平分线,求∠COD的度数.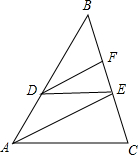 如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,
如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,