题目内容
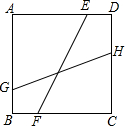 如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=
如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正方形的性质
专题:
分析:过点B作BK∥EF交AD于K,作BM∥GH交CD于M,可得∠KBM=45°,作∠MBN=45°交DC的延长线于N,求出∠ABK=∠CBN,然后利用“角边角”证明△ABK和△CBN全等,根据全等三角形对应边相等可得BN=BK,AK=CN,利用勾股定理列式求出AK,过点M作MP⊥BN于P,可得△BMP是等腰直角三角形,设GH=BM=x,表示出MP,然后利用∠N的正切值列出方程求解即可.
解答:解:如图,过点B作BK∥EF交AD于K,作BM∥GH交CD于M,
则BK=EF=
,BM=GH,
∵线段GH与EF的夹角为45°,
∴∠KBM=45°,
∴∠ABK+∠CBM=90°-45°=45°,
作∠MBN=45°交DC的延长线于N,
则∠CBN+∠CBM=45°,
∴∠ABK=∠CBN,
在△ABK和△CBN中,
,
∴△ABK≌△CBN(ASA),
∴BN=BK,AK=CN,
在Rt△ABK中,AK=
=
=1,
过点M作MP⊥BN于P,
∵∠MBN=45°,
∴△BMP是等腰直角三角形,
设GH=BM=x,则BP=MP=
BM=
x,
∵tan∠N=
=
,
∴
=
,
解得x=
,
所以GH=
.
故选B.
则BK=EF=
| 5 |
∵线段GH与EF的夹角为45°,
∴∠KBM=45°,
∴∠ABK+∠CBM=90°-45°=45°,
作∠MBN=45°交DC的延长线于N,
则∠CBN+∠CBM=45°,

∴∠ABK=∠CBN,
在△ABK和△CBN中,
|
∴△ABK≌△CBN(ASA),
∴BN=BK,AK=CN,
在Rt△ABK中,AK=
| BK2-AB2 |
(
|
过点M作MP⊥BN于P,
∵∠MBN=45°,
∴△BMP是等腰直角三角形,
设GH=BM=x,则BP=MP=
| ||
| 2 |
| ||
| 2 |
∵tan∠N=
| BC |
| CN |
| MP |
| PN |
∴
| 2 |
| 1 |
| ||||||
|
解得x=
2
| ||
| 3 |
所以GH=
2
| ||
| 3 |
故选B.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的性质,锐角三角函数的定义,熟记各性质并作辅助线构造出全等三角形和等腰直角三角形是解题的关键.

练习册系列答案
相关题目
在平面中,下列命题为真命题的是( )
| A、四个角相等的四边形是矩形 |
| B、对角线互相垂直的四边形是菱形 |
| C、对角线相等的四边形是矩形 |
| D、四边都相等的四边形是正方形 |
 如图,△ABC内接于⊙O,∠A=60°,BC=4
如图,△ABC内接于⊙O,∠A=60°,BC=4| 3 |
 |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
 如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP2:DQ2等于( )
如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP2:DQ2等于( )| A、9:16 | B、13:10 |
| C、13:24 | D、12:13 |
下列各式中,一定成立的是( )
A、(-
| ||
B、
| ||
C、
| ||
D、
|
 如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题:
如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题: 如图,AB=8cm,BC=7cm,AC=6cm,BE=CE,那么CD=
如图,AB=8cm,BC=7cm,AC=6cm,BE=CE,那么CD= 如图,折叠宽度相等的长方形纸条,若∠1=65°,则∠2=
如图,折叠宽度相等的长方形纸条,若∠1=65°,则∠2= 如图,△ABC的面积为12,BD=2DC,AE=EC,那么阴影部分的面积是
如图,△ABC的面积为12,BD=2DC,AE=EC,那么阴影部分的面积是