题目内容
 如图,AB=8cm,BC=7cm,AC=6cm,BE=CE,那么CD=
如图,AB=8cm,BC=7cm,AC=6cm,BE=CE,那么CD=考点:相似三角形的判定与性质,全等三角形的判定与性质,角平分线的性质,勾股定理
专题:
分析:根据等弦所对的圆周角相等,可得∠DCE与∠CAE的关系,∠DBE与∠BAE的关系,根据相似三角形的判定与性质,可得
=
,
=
,再根据等量代换,可得答案.
| CD |
| AC |
| DE |
| CE |
| DB |
| AB |
| DE |
| BE |
解答:解:∵BE=CE,
∴∠DCE=∠CAE,∠DBE=∠BAE.
∵∠CED=∠CEA,∠DCE=∠CAE,
∴△CDE∽△ACE,
=
,
∵∠DEB=BEA,∠DBE=∠BAE,
∴△EDB∽△EBA,
=
,
∵BE=CE,
∴
=
令CD=x,DB=7-x
=
,
解得x=CD=3cm,
故答案为:3cm.
∴∠DCE=∠CAE,∠DBE=∠BAE.
∵∠CED=∠CEA,∠DCE=∠CAE,
∴△CDE∽△ACE,
| CD |
| AC |
| DE |
| CE |
∵∠DEB=BEA,∠DBE=∠BAE,
∴△EDB∽△EBA,
| DB |
| AB |
| DE |
| BE |
∵BE=CE,
∴
| CD |
| AC |
| DB |
| AB |
令CD=x,DB=7-x
| x |
| 6 |
| 7-x |
| 8 |
解得x=CD=3cm,
故答案为:3cm.
点评:本题考查了相似三角形的判定与性质,利用了等弦的性质,相似三角形的判定与性质,关键是确定相似三角形相似的条件,题目较难.

练习册系列答案
相关题目
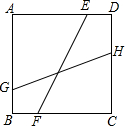 如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=
如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分式
的分子分母都加1,所得的分式
的值比
( )
| x+1 |
| 2x-1 |
| x+2 |
| 2x |
| x+1 |
| 2x-1 |
| A、减小了 | B、不变 |
| C、增大了 | D、不能确定 |
 如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的主视图的面积是
如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的主视图的面积是 如图,长方形中两个相邻的正方形,其面积分别为4和3,那么阴影部分的面积是
如图,长方形中两个相邻的正方形,其面积分别为4和3,那么阴影部分的面积是