题目内容
20.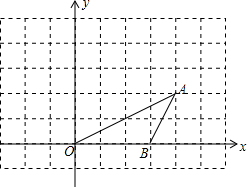 如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°到△OA′B′.
如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°到△OA′B′.(1)画出△OA′B′;
(2)点A′的坐标为(-2,4);
(3)求:△OAB中OA边上的高.
分析 (1)根据图形旋转的性质画出图形即可;
(2)根据点A′在坐标系中的位置写出A′的坐标即可;
(3)根据勾股定理求出OA′的长,再由三角形的面积公式即可得出结论.
解答 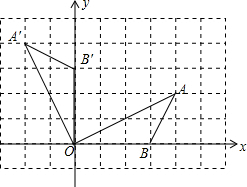 解:(1)如图所示;
解:(1)如图所示;
(2)由图可知,A’(-2,4).
故答案为(-2,4);
(3)∵OA′=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴h=$\frac{3×2}{2\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$.
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
相关题目
5.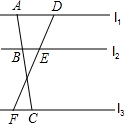 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )
 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )| A. | 3 | B. | $\frac{12}{5}$ | C. | $\frac{18}{5}$ | D. | $\frac{5}{2}$ |
10.下列结论中,不正确的是( )
| A. | 两点确定一条直线 | |
| B. | 等角的余角相等 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 两点之间,线段最短 |
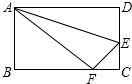 如图,已知矩形ABCD中,AB=8cm,BC=10cm,在边CD上取一点F,将△ADF折叠使点D恰好落在BC边上的点E,则CF的长为4.
如图,已知矩形ABCD中,AB=8cm,BC=10cm,在边CD上取一点F,将△ADF折叠使点D恰好落在BC边上的点E,则CF的长为4.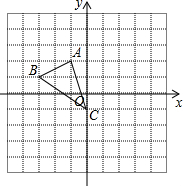 已知△ABC在坐标系中的位置如图:
已知△ABC在坐标系中的位置如图: