题目内容
若n边形的每个内角都等于150°，则n=_____．
12
【解析】试题解析：由题意可得：
解得
故多边形是12边形．
故答案为：12．
练习册系列答案
相关题目
―抛物线与x轴的交点是A(－2，0)，B(1，0)，且经过点C(2，8)．
(1)求该抛物线的解析式；
(2)求该抛物线的顶点坐标．
(1) y＝2x2＋2x－4(2)(－，－ )
【解析】分析:（1）因为已知抛物线与x轴两交点坐标，则设交点式y=a(x+2)(x-1，然后把c(2,8代入求出a即可；（2）把（1）中的函数解析式转化为顶点式，可以直接得到答案.
本题解析：
(1)设这个抛物线的解析式为y=ax2＋bx＋c．将A(－2，0)，B(1，0)，C(2，8)三点代入，得解这个方程组，得∴所求抛物线的解析... ( 本小题满分10分)如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：
⑴△AEH≌△CGF；
⑵四边形EFGH是菱形．
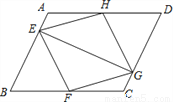
（1）证明见试题解析；（2）证明见试题解析．
【解析】试题分析：(1)、由全等三角形的判定定理SAS证得结论；(2)、易证四边形EFGH是平行四边形，那么EF∥GH，那么∠HGE=∠FEG，而EG是角平分线，易得∠HEG=∠FEG，根据等量代换可得∠HEG=∠HGE，从而有HE=HG，易证四边形EFGH是菱形．
试题解析：（1）、如图，∵四边形ABCD是平行四边形， ∴∠A=∠C，
... 如图，在?ABCD中，AB＝4，BC＝6，AC的垂直平分线交AD于点E，则△CDE的周长是( )
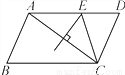
A. 7 B. 10 C. 11 D. 12
B
【解析】试题分析：根据线段垂直平分线的性质可得AE=EC，再根据平行四边形的性质可得DC=AB=4，AD=BC=6，进而可以算出△CDE的周长．
【解析】
∵AC的垂直平分线交AD于E，
∴AE=EC，
∵四边形ABCD是平行四边形，
∴DC=AB=4，AD=BC=6，
∴△CDE的周长为：EC+CD+ED=AD+CD=6+4=10，
故选：B．
... 正十边形的每个外角为________
36°
【解析】正十边形的一个外角为：360°÷10=36°，
故答案为：36°. 四边形ABCD中，若∠A+∠C+∠D=280°，则∠B的度数为( )
A. 80° B. 90° C. 170° D. 20°
A
【解析】试题分析：四边形的内角和为360°，
∴∠B＝360°－(∠A＋∠C＋∠D)
＝360°－280°
＝80°，
故选A． 如果一个多边形的内角和是720°，那么这个多边形的对角线的条数是（ ）
A. 6 B. 9 C. 14 D. 20
B
【解析】设多边形的边数为n，则有：(n-2)•180°=720°，解得：n=6，
所以这个多边形的对角线的条数是==9，
故选B. 已知x-y=4xy，则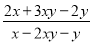
的值为________.
【解析】因为 则= .
故答案： 已知x为整数,且分式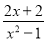
的值为整数,则x可取的值有( )
A.1个 B.2个 C.3个 D.4个
D
【解析】本题考查的是分式的性质
先化简分式，再根据分式的性质分析即可。
,
当分别等于2，1，-1或-2，即x分别等于3，2，0或-1时，分式的值为整数.
故选D。