Question

1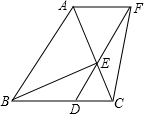．如图，已知△ABC是等边三角形，D、E 分别在边BC、AC上，且CD=CE，连结DE并延长至点F，使EF=AE，连结AF、BE和CF．
（1）求证：四边形ABDF是平行四边形．
（2）若AB=6，BD=2DC，求四边形ABDF的面积．

Answer 1

分析 （1）由∠AEF=∠CED=60°，EF=EA，得出△AEF为等边三角形，由内错角相等，两直线平行得出AF∥BD，得出AF=BD，由平行四边形的判定定理即可得出结论；
（2）过点A作AH⊥BC于H，得出∠BAH=30°，利用含30°直角三角形的性质，得出BH=$\frac{1}{2}$AB=3，利用勾股定理可得出AH，根据AB=6，BD=2DC，求出BD，即可得出结论．

解答 （1）证明：∵∠AEF=∠CED=60°，EF=EA，
∴△AEF为等边三角形，
∴∠AFE=∠FDC=60°，
∴AF∥BD，
∵AF=AE=AC-CE=BC-CD=BD，
∴AF∥BD且AF=BD，
∴四边形ABDF为平行四边形；
（2）解：过点A作AH⊥BC于H，如图所示：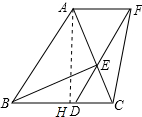
在Rt△ABH中，
∠BAH=90°-∠ABH=30°，
∴BH=$\frac{1}{2}$AB=3，AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$，
∵△ABC是等边三角形，AB=6，BD=2DC，
∴BD=4，
∴S_{四边形ABDF}=BD•AH=4×3$\sqrt{3}$=12$\sqrt{3}$．

点评 本题主要考查了等边三角形的性质及判定，平行四边形的判定，含30°直角三角形的性质，综合运用各种判定定理，作出适当的辅助线是解答此题的关键．